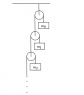
John1951 said:
Homework Statement
OK, I've worked up my nerve to ask a stupid question about this problem. I've read the various discussions of it, but I'm clearly missing something.[/B]
m
0 = 1/(1-t), m
i= t^(i-1) for i > 0.
Homework Equations
The right-hand mass is 1/(1-t). The sum of the left-hand masses (an infinite series) is also 1/(1-t).
The Attempt at a Solution
Therefore, the weight on both sides of the top pulley is equal and a = 0.
This clearly is not true, so where did I go wrong?
Thanks!
What possible range of values for ##\ t\ ## make sense in regard to ##\ m_0, m_1, m_2, \dots\ ## being masses?
If ##\ t>1\,,\ ## then ##\ m_0\ ## would be negative. Can't have that.
If ##\ t=1\,,\ ## then ##\ m_0\ ## would be undefined. Can't have that.
If ##\ t<0\,,\ ## then ##\ m_i\ ## would be negative for even values of ##\ i\,,\ i>0\ ##. Can't have that.
If ##\ t=0\,,\ ## then ##\ m_i\ ## would be zero for ##\ i>0\ ##. So, clearly the statement is false in this case.
Therefore, you need to check this situation for ##\ 0<t<1\ .\ ##
To see how this all works, try the case of t = 0.5 .
Added in
Edit:
Actually, t = 0.5 is not a representative case. It's a special case. Try it anyway.