- #1
John1951
- 9
- 0
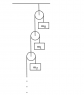
Homework Statement
OK, I've worked up my nerve to ask a stupid question about this problem. I've read the various discussions of it, but I'm clearly missing something.2. Homework Equations [/B]
The right-hand mass is 1/(1-t). The sum of the left-hand masses (an infinite series) is also 1/(1-t).
The Attempt at a Solution
Therefore, the weight on both sides of the top pulley is equal and a = 0.
This clearly is not true, so where did I go wrong?
Thanks!