SUMMARY
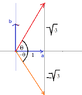
The discussion centers on determining the possible values of the scalar \( x = \vec{b} \cdot \vec{c} \) when the vectors \( \vec{a}, \vec{b}, \vec{c} \) are linearly dependent in a three-dimensional real vector space. Given the conditions \( \vec{a} \cdot \vec{a} = \vec{b} \cdot \vec{b} = \vec{a} \cdot \vec{c} = 1 \), \( \vec{a} \cdot \vec{b} = 0 \), and \( \vec{c} \cdot \vec{c} = 4 \), the analysis reveals that the possible values for \( x \) are \( 2 \) and \( -2 \) based on the angles \( \theta = 0 \) and \( \theta = \pi \). The discussion emphasizes the importance of understanding vector relationships and the implications of linear dependence.
PREREQUISITES
- Understanding of vector operations, specifically dot products and cross products.
- Knowledge of linear dependence and independence in vector spaces.
- Familiarity with three-dimensional geometry and vector representation.
- Basic trigonometry, particularly the cosine function and angles between vectors.
NEXT STEPS
- Study the properties of linear dependence and independence in vector spaces.
- Learn about the scalar triple product and its applications in determining vector relationships.
- Explore the geometric interpretation of dot products and their implications in three-dimensional space.
- Investigate the relationship between angles and vector magnitudes in the context of linear algebra.
USEFUL FOR
Students of linear algebra, mathematicians, and anyone involved in physics or engineering who needs to understand vector relationships and linear dependence in three-dimensional space.