Avibu
- 4
- 0
I am facing some difficulties solving one of the questions we had in our previous exam. I am sorry for the bad translation , I hope this is clear.
In each section, find all approppriate matrices 2x2 (if exists) , which implementing the given conditions:
[/B]
I tried to build equations for the first section but I have no idea how to keep from there :
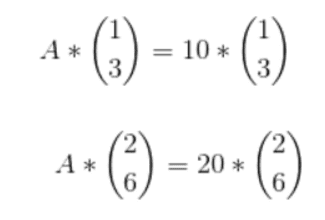 Can you please assist ?
Can you please assist ?
Thanks.
In each section, find all approppriate matrices 2x2 (if exists) , which implementing the given conditions:
-
is an eigenvector of A with eigenvalue of 10 , andis an eigenvector of A with eigenvalue of 20
- is an eigenvector of A with eigenvalue of 10 , and EXISTS eigenvector of A with eigenvalue of 20
The Attempt at a Solution
[/B]
I tried to build equations for the first section but I have no idea how to keep from there :
Thanks.