- #1
arhzz
- 260
- 52
- Homework Statement
- Find the transition matrix
- Relevant Equations
- -
Hello! I have the following matrix (picture 1.)and I am susposed to find the transition matrix ($$ \phi $$) now for that I need the eigenvalue and vectors of this matrix A. The eigenvalues are 1,1 and 2. The eigenvectors I have found to be (1 0 0) (1 1 0) (5 3 1). Now to find the transition matrix we are given this formula(picture 2) where V is a matrix comprised of my eigenvectors and V^-1 simply the inverse. And what the middle one is the part I am having problems with. This phi wave lets call it, is susposed to be the following. In a case of where you have more than one eigenvalue that is the same ( in my case 1 is double) and where the geometrical value of those eigenvalues is 1. Phi wave is calculated like this(picture) where S is the Jordan form of the matrix and beta (this weird looking b) are the eigenvectors of the matrix. Now I dont know how to construct this,even though it might seem straight forward. What is confusing me is I know that lambda is the eigenvalue but,I have 3 where am I susposed to put the third one,what I mean by that is the lambda in the picture is I am assuming reffering to the 1 (the double eigenvalue) but how what do I do with the 2? When you multiply the Jordan form with t and proceed to multiply with V and V-1 you dont get the solution. Also I have tried reading this schematic and I am pretty sure that the Matrix we need to multiply with e is simply the first 3 rows and coloumns. So basically its going to be exactly what is in this picture but the under the t should be a 1. But no matter how I multiply with e and the eigenvalue,regardless of the "combination" I cannot get to the solution.(picture 4). Thanks for the help in advance!
Picture 1. The matrix that is given to me
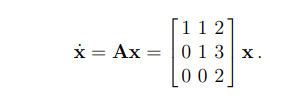
Picture 2. The formula to calculate Phi
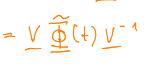 Picture 3.How to construct Phi wave
Picture 3.How to construct Phi wave
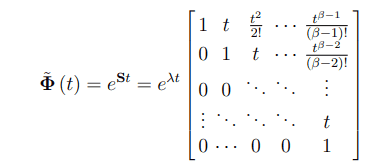 Picture 4. Solution
Picture 4. Solution
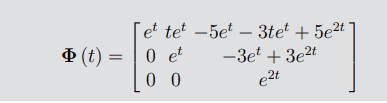
Picture 1. The matrix that is given to me
Picture 2. The formula to calculate Phi
Last edited: