Find angular momentum, energy, and distance of closest approach

[oddjobmj]

Homework Statement

A particle with mass=m moves in the xy plane. It is under the influence of a repulsive central force described by:

F(r)={A$\hat{r}$ if r<R₀ and 0 if r>R₀}

$\hat{r}$ is the unit radial vector and R₀ is the range of the force

The initial conditions are x=-3 R₀, y=0.5 R₀, V_x=w, v_y=0

(A) Calculate energy and angular momentum in terms of the parameters A, R₀, and w.

(B) Calculate the approximate distance of closest approach to the origin in terms of A, R₀, and w, accurate to the order A assuming A is small.

Homework Equations

Energy=U+K=$\frac{1}{2}$mv²+Force*Distance
Angular momentum=mvrsin$\theta$

The Attempt at a Solution

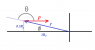
I am having a hard time visualizing this problem. My current take is represented in the linked image:

http://imgur.com/8btZdls (I forgot the negative on -3R₀)

Does that look correct?

(A)
You could represent the energy of the particle by $\frac{1}{2}$mv²+A(R₀-r) if the particle is within the range of the force (r<R₀) but it starts outside that range meaning it only has kinetic energy. Am I to answer with regard to its current energy or generally?

Currently energy = $\frac{1}{2}$mw²

Angular Momentum=mwrsin(theta) but I am asked to represent this value in terms of the parameters A, R₀, and w. I can write in terms of R₀ by providing a variable multiple of R₀ as r where R₀*$\alpha$=r thus:

mw$\alpha$R₀sin$\theta$

Does that seem like the answer I am looking for?

(B)
Is this asking, given the initial velocity w and its initial position, how close would the particle come to the origin? i.e. it travels in the positive x direction until reaching the range of affect of the force A and then takes a curved path away from the origin. Find the nearest distance along that path to the origin?

Thank you for your help!

 

[TSny]

Regarding (A), do you think energy and/or angular momentum is conserved as the particle travels along?

Your interpretation of (B) seems correct to me.

 

[oddjobmj]

Thank you. Yes, they are conserved. The equation to represent them just looks differently depending on the particles location. You are obviously trying to hint at something though. Maybe I'm just too blunt to pick it up. :tongue:

Also, with respect to (B) if my equation above is correct for r<R₀ I could set potential = to -kinetic initial and solve for r. The problem is that the particle probably never steps and changes direction but rather takes a curved path such that all the energy of the particle is never fully transferred to potential energy so -A(R₀-r) will never equal $\frac{mw^2}{2}$ and that equation does not contain t as a variable so I'm not sure where to go from here.

I guess it does say approximate and assume A is small. Straight line?

 

[TSny]

Thank you. Yes, they are conserved. The equation to represent them just looks differently depending on the particles location. You are obviously trying to hint at something though.

You asked about whether you should calculated the energy "currently" (i.e., initially) or "generally". If energy is conserved, does it matter at what point you calculate it?

Also, with respect to (B) if my equation above is correct for r<R₀ I could set potential = to -kinetic initial and solve for r.

You can set KE = -PE only if the total energy is 0. But the particle starts out with positive energy and energy is conserved.

The problem is that the particle probably never steps and changes direction but rather takes a curved path such that all the energy of the particle is never fully transferred to potential energy so -A(R₀-r) will never equal $\frac{mw^2}{2}$ and that equation does not contain t as a variable so I'm not sure where to go from here.

Right, the particle will travel a curved path. But at the point of closest approach, there is something special about the relative orientation of the velocity vector and the position vector. This will help simplify the expression for angular momentum at that point. Try to use your conservation laws to relate the energy and angular momentum at the point of closest approach to the energy and angular momentum that you start with.

 

[TSny]

I guess it does say approximate and assume A is small. Straight line?

That's too much approximation That would be the "zeroth"" order approximation in the small quantity A for the distance of closest approach. You want to try to get the "first-order" approximation.

 

[oddjobmj]

You asked about whether you should calculated the energy "currently" (i.e., initially) or "generally". If energy is conserved, does it matter at what point you calculate it?

Yes, I'm sorry. I see what you are getting at. No, the energy is the conserved throughout but we are never given values for m and v, for example. The description of the energy is different depending on the location. It starts off with all kinetic and no potential. Once it enters the... force field... it will lose kinetic and gain potential. I would use a general equation, i.e. one that works for t=0 -> ∞, but the R₀-r portion would break down if r were greater than R₀. Instead, I could write a conditional description much like they have with the description of F(r) unless you think there is a more obvious way of doing it.

You can set KE = -PE only if the total energy is 0. But the particle starts out with positive energy and energy is conserved.

Great point, thanks!

Right, the particle will travel a curved path. But at the point of closest approach, there is something special about the relative orientation of the velocity vector and the position vector. This will help simplify the expression for angular momentum at that point. Try to use your conservation laws to relate the energy and angular momentum at the point of closest approach to the energy and angular momentum that you start with.

I will have to think on this. I wanted to say that they would be equivalent but that can't be the case because if the velocity is such that it follows a (nearly) straight line through the field the velocity vector would always be greater than the position vector (and particularly so at the point of interest). That brings up an interesting point though. At that point the vectors are perpendicular. That also seems to be the case at other locations.

That's too much approximation That would be the "zeroth"" order approximation in the small quantity A for the distance of closest approach. You want to try to get the "first-order" approximation.

Hey, it was worth a shot.

 

[TSny]

Since the energy has the same value at each point of the trajectory, you can evaluate it at the initial position. You have shown how to express it in terms of m and w. Likewise, you should be able to express the angular momentum at the starting point in terms of m, w, and R_o. This is what I assumed they wanted in (A). I could be misinterpreting it though.

For part (B) you will need to consider how to write the energy and angular momentum at the point of closest approach in terms of the speed and distance from the origin at that point.

 

[oddjobmj]

Since the energy has the same value at each point of the trajectory, you can evaluate it at the initial position. You have shown how to express it in terms of m and w. Likewise, you should be able to express the angular momentum at the starting point in terms of m, w, and R_o. This is what I assumed they wanted in (A). I could be misinterpreting it though.

For part (B) you will need to consider how to write the energy and angular momentum at the point of closest approach in terms of the speed and distance from the origin at that point.

My understanding is that mwrsinθ=Angular Momentum. Are you saying I should be able to get rid of theta?

EDIT:

mwαR₀sinθ is what I came up with, actually. Where R₀α=r and w=v₀ I guess I could solve for alpha provided the initial conditions. It is hard to tell what they are asking for though.

$\sqrt{9.25}$R₀mwsinθ

EDIT 2:

I'm not sure how angular momentum and energy equate. This is probably something really obvious. Am I supposed to be using the relativistic energy-momentum relation? That seems like a stretch to me.

 

[voko]

As TSny said, at the point closest to the center, there is something special about the direction of velocity. Think about the velocity as a vector, which is a sum of two orthogonal components: one is the velocity toward the center, another is perpendicular to it. What happens with these at the point of interest?

What is the angular moment in that case?

 

[oddjobmj]

Ah, well put Voko, thank you.

What center are we talking about? We can't be talking about the origin of our coordinate system, right? If we are then the diagram I drew is incorrect. The arc formed by the path this particle takes is somewhere off in quadrant two of our coordinate system. One vector would be tangent to this curve and the other perpendicular to that but pointing out into quadrant 2, not at the origin of our coordinate system. The force within the force field is repulsive, not attractive, much like the faces I make when I can't figure out a problem.

Either way, the velocity vector formed at that point would be perpendicular to the line between our particle and the origin. Beyond that I can't put my finger on anything special. They won't necessarily be equivalent.

What am I missing?

 

[voko]

Yes we are talking about the origin of the coordinate system - the force is defined in terms of a vector from it. And I can't see how that will invalidate your diagram.

You are quite correct stating that at the closest approach the velocity will be perpendicular with the vector from the origin. That makes the expression for angular momentum especially simple: what is it? What does its conservation give you?

 

[oddjobmj]

Ah, I kept looking to the angle formed between r and the x-axis for theta in the angular momentum function when I should have been looking at the angle between p and r (I believe) which is 90 degrees in this case thus simplifying angular momentum to mvr.

What is even more confusing is why this helps me find r. That component of angular momentum and r are in the same direction but I honestly have no idea how they connect. I usually start by scratching out some equations which helps give some perspective but I'm getting nowhere.

 

[voko]

Now that you have the angular momentum at the closest approach, apply conservation of angular momentum (you know the initial angular momentum). That will give you one equation relating $r$ and $v$.

You still need one other equation to complement that and find $r$. What could that other equation be? Hint: TSny gave you some very good hints previously :)

 

[oddjobmj]

I appreciate your help, thank you.

mvr=$\sqrt{9.25}$R₀wsinθ

Solving for v:

v=($\sqrt{9.25}$R₀wsinθ)/r

$\frac{1}{2}$mw²=$\frac{1}{2}$mv²+A(R₀-r)

Solving for r:

r=$\frac{2AR+mv^2-mw^2}{2A}$

I can then plug in my equation for v into the equation for r to find r with respect to A, R, and w. Is that what you were thinking?

EDIT: My concern is that I am told to approximate this distance accurate to the order A. This is an exact solution. What am I doing wrong?

 

[TSny]

I appreciate your help, thank you.

mvr=$\sqrt{9.25}$R₀wsinθ

Solving for v:

v=($\sqrt{9.25}$R₀wsinθ)/r

OK. But you should be able to simplify this by substituting an expression for sinθ.

$\frac{1}{2}$mw²=$\frac{1}{2}$mv²+A(R₀-r)

Solving for r:

r=$\frac{2AR+mv^2-mw^2}{2A}$

OK. But I wouldn't solve for r yet. When you substitute for v, you will bring in another term that depends on r. So, you would just have to solve for r all over again.

EDIT: My concern is that I am told to approximate this distance accurate to the order A. This is an exact solution. What am I doing wrong?

You will see that you will end up with a cubic equation for r that will be messy to solve. But you can still get an approximation that will be good for small A.

 

[oddjobmj]

OK. But you should be able to simplify this by substituting an expression for sinθ.

I was wondering about that. Sure, sinθ=O/H, but what are these two legs? Originally there is only one vector which is parallel with the x-axis. sinθ=0 Alternatively, I could use the legs of the triangle formed by position of the particle and the origin but then when I get to the point of interest sin would not simplify to 1 because the angle would not be 90 degrees.

 

[TSny]

$\vec{L} = \vec{r} \times \vec{p}$

$\vec{r}$ is the position vector of the particle relative to the origin of the coordinate system.
$\vec{p}$ is the linear momentum of the particle.

So, the magnitude of the angular momentum is $L = rp \sin \theta$ where $\theta$ is the angle between $\vec{r}$ and $\vec{p}$.

You should be able to simplify $r \sin \theta$ for the initial position of the particle.

Or, you could write out $\vec{r}$ in Cartesian coordinates for the initial position and also write out $\vec{p}$ in Cartesian coordinates and do the cross product to find $\vec{L}$ at the initial position.

You also know the value of $\theta$ at the position of closest approach, so that will make it easy to write $L$ at the final position.

 

[oddjobmj]

L_i=rmwsinθ

sinθ=$\frac{3}{\sqrt{9.25}}$

r=$\sqrt{9.25}$R₀

So, L_i=3R₀mw

L_f=rmv because sin(90)=1

v=3R₀w/r

Because momentum is conserved rmv=3R₀mw => rv=3R₀w

I also still have $\frac{1}{2}$mw²=$\frac{1}{2}$mv²+A(R₀-r)

Plug v=3R₀w/r in for v and solve for r and chaos ensues.

$\frac{mw^2}{2}$=$\frac{m}{s}$($\frac{3R_0w}{r}$)²+A(R₀-r)

 

[TSny]

L_i=rmwsinθ

sinθ=$\frac{3}{\sqrt{9.25}}$

I don't think the 3 in the numerator is correct.

Plug in for v and solve for r and chaos ensues.

Yes, chaos ensues. You'll need to calm the waters by treating A as "small" and making appropriate approximations.

 

[oddjobmj]

Genius!

I see, are we thinking the 1/2 leg instead of the 3? The opposite the small angle is .5 so sin in that respect would be .5/sqrt(9.25) but for some reason I was thinking we were looking for the other angle. Gah...

Anyway, if we consider A negligible then the A(R₀-r) drops out and our equation becomes

w²=m($\frac{R_0w}{2r}$)²

Solve that for r:

r=$\frac{Rsqrt(m)}{2}$

That doesn't seem right because r is then not dependent on initial velocity. But then I guess it wouldn't be because we are considering the force from the field to be negligible but if that's the case then why doesn't it travel in a straight line? The answer would be the y component of the initial position.

 

[TSny]

I see, are we thinking the 1/2 leg instead of the 3? The opposite the small angle is .5 so sin in that respect would be .5/sqrt(9.25) but for some reason I was thinking we were looking for the other angle. Gah...

θ is the angle between the r direction and the p direction, as shown in the figure. How does sinθ compare with sin∅, where ∅ is the angle that r makes to the -x axis?

Anyway, if we consider A negligible then the A(R₀-r) drops out ...

You're back to the "zeroth" order approximation. We don't want to go that far.

 

[oddjobmj]

θ=180-∅
∅=sin^-1($\frac{1}{2sqrt(9.25)}$)

θ=180-sin^-1($\frac{1}{2sqrt(9.25)}$)

I can find a decimal approximation of the angle. Not sure how to simplify the exact definition.

Should A=1 then? I remember orders with respect to series expansions but I am not familiar with such approximations outside that clearly defined context.

 

[TSny]

θ=180-∅

Right. θ and ∅ are supplementary angles. So, how are sinθ and sin∅ related?

Then note that from the diagram, sin∅ = .5/r.

What do you now get for the initial angular momentum in terms of R_o and w? I think you should get what you got before except with the 3 replaced by .5

Thus, what is the correct expression for v in terms of r at the point of closest approach?

Should A=1 then? I remember orders with respect to series expansions but I am not familiar with such approximations outside that clearly defined context.

In order to see how to get the first order approximation, let's start with your energy equation after you substitute for v in terms of r.

 

[oddjobmj]

That makes sense, thank you.

v=$\frac{R_0w}{2r}$

$\frac{mw^2}{2}$=$\frac{m(R_0w/(2r))^2}{2}$+A(R₀-r)

 

[TSny]

Good. Almost home. (I think)

All these symbols are making me dizzy. Let's let $a = mw^2/2$ and $b = mR_0^2w^2/8$. We can always sub back at the end.

Check to see that we can then write your equation as $$a = \frac{b}{r^2} + A(R_0-r)$$
(I'm feeling better already!)

Now, we want a solution for $r$ that is accurate to first order in $A$. So, all we need to do is keep the terms accurate to first order in $A$. Note that the second term on the right already has a factor of $A$. That means, that we can use a zeroth order approximation for the quantity inside the parentheses and that term will still be accurate to first order in $A$! So, inside those parentheses we can just use the zeroth-order approximation for r. Can you see what the zeroth order approximation for $r$ is? It's the minimum distance of approach if we turn off the force completely!

 

[oddjobmj]

Ah yes, .5R₀ would be the minimum provided the initial position and velocity.

 

[TSny]

Good. Now you can solve for r and simplify to first order in A.

 

[oddjobmj]

Substitute .5R₀ in for r on the right and then solving for r gets me:

r=sqrt($\frac{2b}{2a-AR_0}$)

Substituting a and b back in I get:

r=$\frac{1}{2}$sqrt($\frac{mR^2w^2}{mw^2-AR}$)

 

[TSny]

Looks good. You can simplify it and still be accurate to first order. See if you can make use of the approximation $1/\sqrt{1-x} \approx 1+x/2$ for small x. First, go ahead and take the square root of the $R^2$ and then divide numerator and denominator inside the square root by $mw^2$.

 

[oddjobmj]

I like the initial simplification.

r=$\frac{R}{2sqrt(1-AR_0)}$

I am comfortable now with the concepts that were touched on and this is how I would/will work out the problem. I must admit, though, that the further simplification for small x is something I would not likely use unless necessary.

Thank you for your advice and guidance!

 

[TSny]

I like the initial simplification.

r=$\frac{R}{2sqrt(1-AR_0)}$

I believe that should be $$r = \frac{R_0}{2\sqrt{1-\frac{AR_0}{mw^2}}}$$
With the approximation of the square root, you have $$r = \frac{R_0}{2}(1+\frac{AR_0}{2mw^2})$$

I am comfortable now with the concepts that were touched on and this is how I would/will work out the problem. I must admit, though, that the further simplification for small x is something I would not likely use unless necessary.

Thank you for your advice and guidance!

OK. Good work.