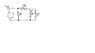Gauss M.D.
- 151
- 1
Homework Statement
Find the current marked I3 in the circuit.
Homework Equations
The Attempt at a Solution
The voltage over R2 and R1 is the same. The current I0 (12mA) is the sum of I2 and I1.
I1*R1 = I2*R2:
4*I1 = 1.25*I2
I1 + I2 = 12 <=> I2 = 12 - I1
4*I1 = 1.25*(12 - I1) = 15 - 1.25I1
5.25*I1 = 15
I1 = 2.86
I think I've messed up already here. Can anyone spot what I'm doing wrong??