Find dy/dx by implicit differentiation

[momogiri]

You mean by time-sing 2xy and x^2 by 2sqrtxy?

 

[bob1182006]

yes and combining the fractions on the top and the bottom you can cancel out 2sqrt(xy) and have just 1 denominator/numerator.

 

[momogiri]

Hmm.. I'm not sure if I did it correctly though, so here it is:
$$\frac{2xy - \frac{1}{2\sqrt{xy}}y}{\frac{1}{2\sqrt{xy}}x - x^{2}}$$
into
$$\frac{\frac{2xy(2\sqrt{xy})}{(2\sqrt{xy})} - \frac{y}{2\sqrt{xy}}}{\frac{x}{2\sqrt{xy}} - \frac{x^{2}(2\sqrt{xy})}{(2\sqrt{xy})}}$$
and into
$$\frac{\frac{2xy(2\sqrt{xy}) - y}{2\sqrt{xy}}}{\frac{x - x^{2}(2\sqrt{xy})}{2\sqrt{xy}}}$$
which becomes
$$\frac{2xy(2\sqrt{xy}) - y}{x - x^{2}(2\sqrt{xy})}$$
and..
$$\frac{4xy(\sqrt{xy}) - y}{x - x^{2}(2\sqrt{xy})}$$?
I donno if I can simplify it more XP

 

[bob1182006]

yes that's about as simplified as you can go

 

[momogiri]

Man, that was a pain.. but.. I got stuck again :P Surprise surprise..

Question:
Find dy/dx by implicit differentiation.
$$e^{x/y} = 2x - y$$

Attempted:
Isn't $$(d/dx)e^{x/y} = e^{x/y}$$?
Well, I went ahead anyway, and figured out
$$(d/dx)2x = 2$$ and $$(d/dx)y = y'$$
Then I um.. rearranged it so it's
$$y' = 2 - e^{x/y}$$
Which is wrong. lol

I'm assuming that $$(d/dx)e^{x/y} \neq e^{x/y}$$ :P Then how do I find it?

 

[bob1182006]

$$(e^u)'=u'e^u$$

so you need to use the quotient rule on x/y and multiply that to e^(x/y)

 

[momogiri]

Damn, lol
I'll try it XD

Dang, I thought I had it right, but I got it wrong :P
Here's what I did..
Quotient rule = $$\frac{g(x)f'(x)-f(x)g'(x)}{(g(x))^{2}}$$
So I plugged in the numbers as usual..
$$\frac{(y)(x')-(x)(y')}{(y)^{2}}$$ which got me $$\frac{(y)-(xy')}{y^{2}}$$
Therefore the whole thing becomes
$$\frac{y-xy'}{y^{2}}e^{\frac{x}{y}} = 2 - y'$$
So I got rid of y^2
$$y-e^{\frac{x}{y}}xy' = 2y^{2} - y^{2}y'$$
then shuffled
$$y-2y^{2} = e^{\frac{x}{y}}xy' - y^{2}y'$$
Thus
$$y-2y^{2} = y'(e^{\frac{x}{y}}x - y^{2})$$
Therefore
$$y' = \frac{y-2y^{2}}{e^{\frac{x}{y}}x - y^{2}}$$...?

What did I do wrong this time :/

 

[bob1182006]

when you got rid of y^2 you didn't keep the parenthesis:
(y-xy')e^(x/y) =/=y-e^(x/y)xy'

so you're just missing a e^(x/y) multiplied to y in the numerator

 

[momogiri]

Eeek, I don't see it..
And by getting rid of y^2, I actually meant timesing it to the other side XD

 

[bob1182006]

$$\frac{(y-xy')e^{\frac{x}{y}}}{y^2}\neq y-e^{\frac{x}{y}}xy'$$
and the y^2 being carried over to the other side.
it should be:

$$ye^{\frac{x}{y}}-xy'e^{\frac{x}{y}}$$

and continuing from there you are only missing that e^(x/y) on your final answer

 

[momogiri]

Thanks for that, bob :D
I've got another question :/
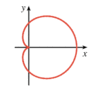
Use implicit differentiation to find an equation of the tangent line to the curve at the point (0, -0.5).
$$x^{2} + y^{2} = (2x^{2} + 2y^{2} - x)^{2}$$

Ok, so $$x^{2} + y^{2} = (2x^{2} + 2y^{2} - x)^{2}$$ becomes $$x^{2} + y^{2} = 2x^{4} + 2y^{4} - x^{2}$$
Which I solved for the d/dx
$$2x + 2yy' = 8x^{3} + 4(2y)^{3}*2y' - 2x$$
Shuffling..
$$2yy' - 4(2y)^{3}*2y' = 8x^{3} - 4x$$
and again
$$y'(2y - 8(2y)^{3}) = 8x^{3} - 4x$$
thus
$$y' = \frac{8x^{3} - 4x}{2y - 8(2y)^{3}}$$ which equals
$$y' = \frac{8x^{3} - 4x}{2y - 64(y)^{3}}$$

Ok. So that's my slope for the tangent line..
And my equation for tangent line is
$$y = \frac{8x^{3} - 4x}{2y - 64(y)^{3}}x$$
and at point (0,-0.5)
$$y + 0.5 = \frac{8x^{3} - 4x}{2y - 64(y)^{3}}x$$
Making it
$$y = \frac{8x^{3} - 4x}{2y - 64(y)^{3}}x - 0.5$$
So I've managed to solve up to here, and.. frankly, I don't know if I'm right XD
Oh, and this is an image they gave me

 

[bob1182006]

no you have $$(2x^2+2y^2-x)^2=(2x^2+2y^2-x)(2x^2+2y^2-x)$$
so you have to multiply that out and then you can do the derivative.

or you can do it straight away $$(u^n)'=nu^{n-1}u'$$
where u=2x^2+2y^2-x

also in order to find the actual slope of the function at (0,-0.5) when you isolate y' plugin (0,-0.5) that way you'll get a number.
so your equation for the line shoudl be: y+0.5=mx

 

[momogiri]

Oh XD Ok

(Off-topic) Hey Bob, will you be on later tonight?
I have to go eat dinner and travel back to my dorm :/ That'll take an hour or two, so...
It'd be great if you're still available to help me after XD

Edit: Daaang, just read your message XD
Oh well, I'll manage somehow :D I appreciate all your help :D

 

[bob1182006]

sorry but I'm sure other people will be able to help too,
just remember that when you need to do product/quotient rule and then do the chain rule if you have (y^n)' where n is different from 1.