member 731016
- Homework Statement
- Please see below
- Relevant Equations
- Please see below
For exercise 3 (2),
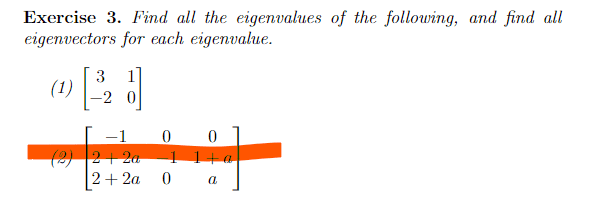 ,
,
The solution for finding the eigenvector is,
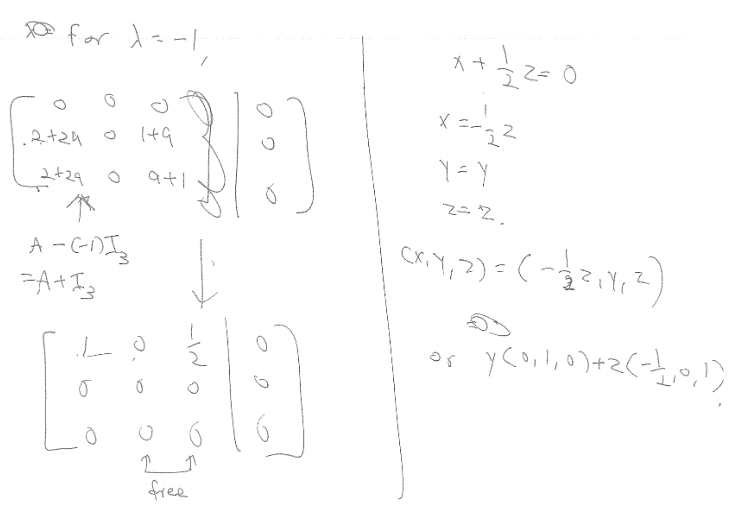
However, I am very confused how they got from the first matrix on the left to the one below and what allows them to do that. Can someone please explain in simple terms what happened here?
Many Thanks!
The solution for finding the eigenvector is,
However, I am very confused how they got from the first matrix on the left to the one below and what allows them to do that. Can someone please explain in simple terms what happened here?
Many Thanks!