Setting Free variables when finding eigenvectors

[Sunwoo Bae]

Homework Statement

Confusion in finding eigenvector? (example shown below)

Relevant Equations

matrix multiplication

upon finding the eigenvalues and setting up the equations for eigenvectors, I set up the following equations.

So I took b as a free variable to solve the equation int he following way.

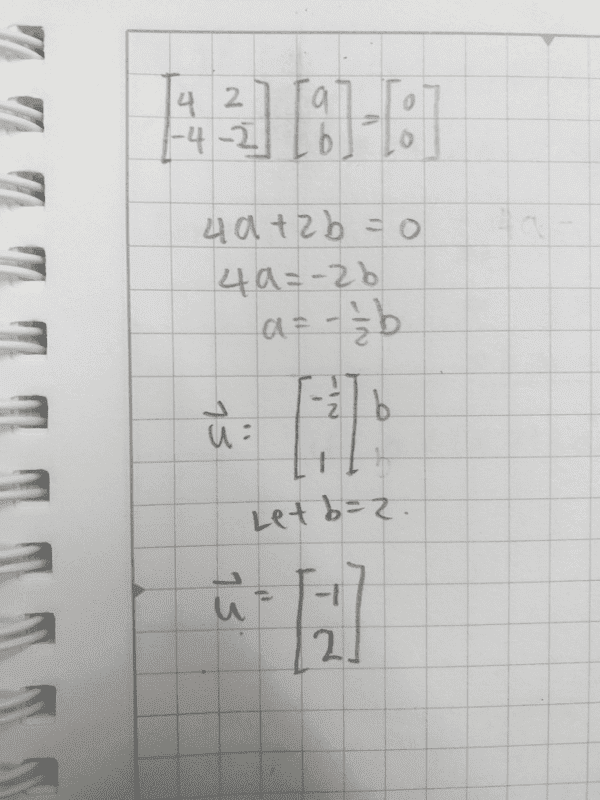
But I also realized that it would be possible to take a as a free variable, so I tried taking a as a free variable too.

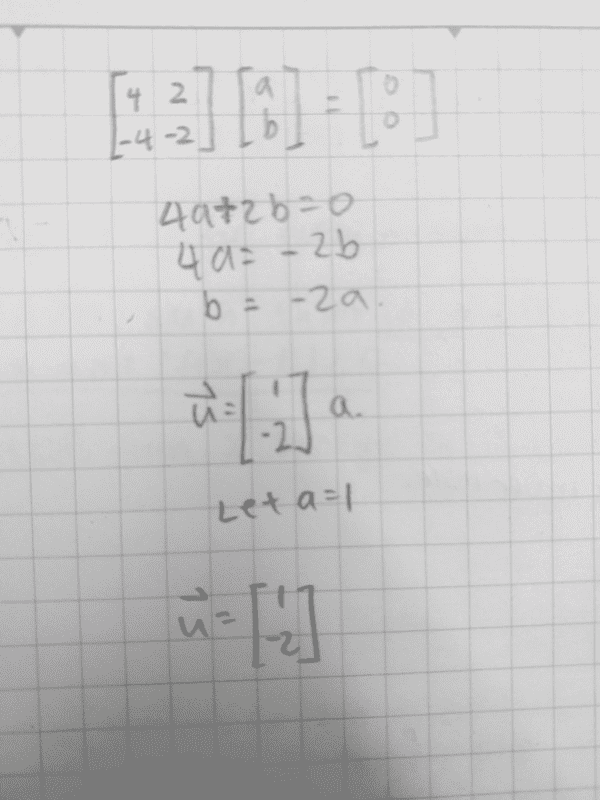
But now I am confused because this results in vectors that is different in sign. Can anyone explain whether I should use a or b as a free variable?

 

[PeroK]

If $\vec u$ is an eigenvector (corresponding to a certain eigenvalue), then $-\vec u$ is also an eigenvector (corresponding to the same eigenvalue). Both your answers are correct.

In general, $c \vec u$ is also an eigenvector for any number $c \ne 0$. Often you choose $c$ such that the eigenvector is normalised - i.e. has length $1$,