Find electric Field through 3 plates using Gausses Law

[Broem]

Homework Statement

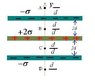
The figure shows three very thin parallel planes of charge with equal separation 8 cm between them. The charge density of the middle plane is +4 nC/m2 (nC = "nano Coulomb") and that of the two outer planes is -2nC/m2. Use Gauss's law to solve the following questions. We choose positive electric field along the y-direction.
What is the Electric Field at point C?

Homework Equations

E=ρD/ε Electric Field at position D

The Attempt at a Solution

I've tried to Calculate the E at distance between The top Positive ρ and the point C and from the bottom ρ to point C. Should these two be equal?
From top:
(4e-9c/m^2 * 0.004m) / ε to give me field to point C

From bottom:
(2e-9c/m^2 * 0.004m) / ε to give field to point C

I know the field results in a - I've tried to add them to get the answer and subtract.
What am I to do from this point?
Am I using the wrong equation?


Thanks!

 

[TSny]

The question asks you to use Gauss' law to find the answer. Since you want the field at point C, you should try to construct a Gaussian surface that goes through C. Choose the shape of the Gaussian surface so that you can take advantage of any symmetry in the problem.