- #1
rocapp
- 95
- 0
See attached image.
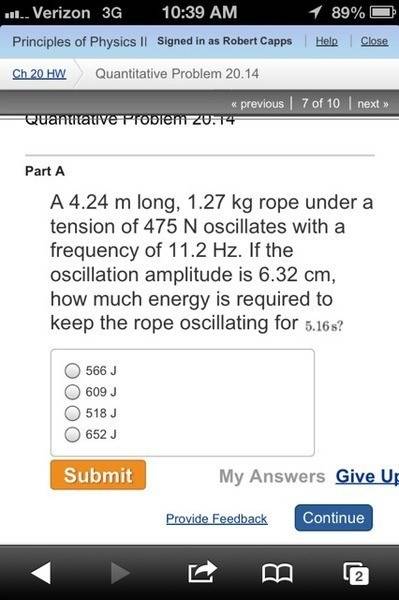
V=sqrt(T/mu)
V=sqrt(T/mu)
Oscillation refers to the repetitive back-and-forth movement of a rope, similar to a pendulum swinging.
In order for a rope to continue oscillating, energy must be continuously applied to overcome friction and maintain the motion.
The energy required for rope oscillation can be affected by factors such as the length and weight of the rope, the amplitude of the oscillation, and the amount of friction between the rope and its supports.
The energy required for rope oscillation can be calculated using the formula E= ½ * k * A^2, where E is the energy, k is the spring constant (related to the stiffness of the rope), and A is the amplitude of the oscillation.
Yes, there is a limit to the energy that can be applied before the rope breaks or the supports fail. This is why it is important to carefully calculate the necessary energy and ensure it is within the limits of the rope and its supports.