Find force with Young's modulus

In summary, the young modulus, also known as the modulus of elasticity, is a measure of the stiffness of a material and is calculated by dividing stress by strain. It is typically expressed in pascals or newtons per square meter and is important in determining a material's ability to resist deformation under stress. Factors such as material type, temperature, and strain rate can affect the young modulus.
  • #1
cbarker1
Gold Member
MHB
349
23
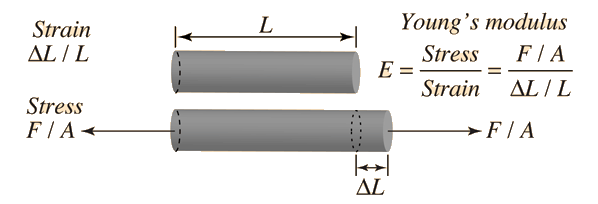
Q: Calculate the force (in N) a piano tuner applies to stretch a steel piano wire 8.50 mm, if the wire is originally 0.850 mm in diameter and 1.35 m long. (Young's modulus for steel is 20.0 ✕ 1010 Pa.)

Work F=Y*A*change in L/L_0

I have no idea what is L_0 and L_f? Please help me.
 
Mathematics news on Phys.org
  • #2
$L = 1.35 \, m$

$\Delta L = 8.5 \times 10^{-3} \, m$

$r = 4.25 \times 10^{-4} \, m$

$E=2.0 \times 10^{11} \, N/m^2$$F = \dfrac{E \cdot \pi r^2 \cdot \Delta L}{L}$

ymod.gif
 

FAQ: Find force with Young's modulus

What is the young modulus?

The young modulus, also known as the modulus of elasticity, is a measure of the stiffness of a material. It is the ratio of stress to strain within the elastic limit of a material.

How do you calculate the young modulus?

The young modulus can be calculated by dividing the stress by the strain. The stress is the force applied per unit area, while the strain is the change in length divided by the original length.

What is the unit of measurement for the young modulus?

The unit of measurement for the young modulus is typically expressed in pascals (Pa) or newtons per square meter (N/m^2). It can also be expressed in gigapascals (GPa) for stronger materials.

Why is the young modulus important?

The young modulus is an important property of a material as it indicates its ability to resist deformation under stress. It is used to determine the strength, stiffness, and elasticity of a material, which can be crucial in engineering and construction projects.

What factors affect the young modulus?

The young modulus can be affected by several factors, including the type of material, temperature, and strain rate. It can also vary for the same material due to different manufacturing processes or impurities present in the material.

Similar threads

Confusion Calculating Young's Modulus
Replies
5
Views
795
Young's modulus — Finding the change in the length of a metal bar under stress
Replies
20
Views
3K
B A statistical definition of Young's Modulus?
Replies
8
Views
2K
Young's modulus, stretching question.
Replies
2
Views
2K
Determining Young's Modulus of Aluminium from Tensile Test
Replies
7
Views
4K
Stretching of a wire due to it's weight
Replies
19
Views
3K
What force should be used to calculate Young's Modulus?
Replies
17
Views
2K
Does Young's Modulus Change When Nano-Tubes Are Connected End-to-End?
Replies
2
Views
1K
Log hanging from 2 steel wires. stress/strain youngs modulus
Replies
8
Views
6K
Calculating Force on a Stretched Steel Rod | Young's Modulus 200*109 Pa
Replies
1
Views
2K

Hot Threads

Recent Insights

Back
Top