chwala
Gold Member
- 2,827
- 415
- Homework Statement
- See attached.
- Relevant Equations
- Mechanics- Pulleys.
I need insight on the highlighted part;
Total height ##= 2h + h + H##
In my understanding, the displacement on either side would be the same, that is ##=h##m given the condition (assumption) that ##a=0##.
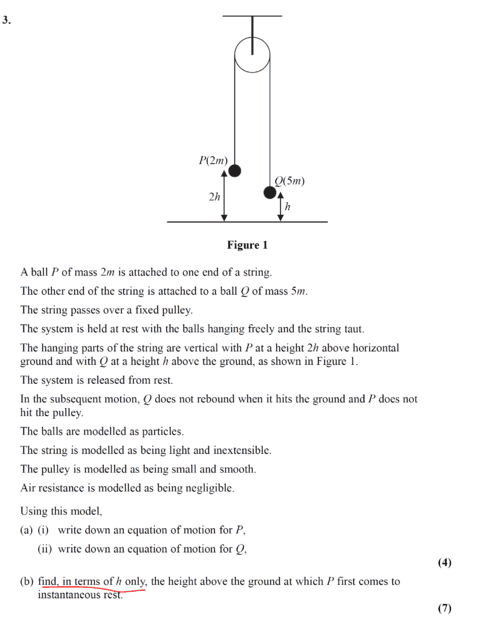

Total height ##= 2h + h + H##
In my understanding, the displacement on either side would be the same, that is ##=h##m given the condition (assumption) that ##a=0##.