Find in the form, ##x+iy## in the given complex number problem

[chwala]

Homework Statement

Find, in the form $x+iy$, the complex numbers given in the polar coordinate form by;

$z=2\left[\cos \dfrac{3π}{4} + i \sin \dfrac{3π}{4}\right]$

Relevant Equations

complex numbers

This is the question as it appears on the pdf. copy;

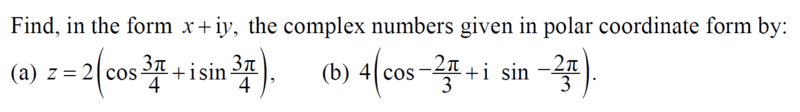
$z=2\left[\cos \dfrac{3π}{4} + i \sin \dfrac{3π}{4}\right]$

My approach;

$\dfrac{3π}{4}=135^0$

$\tan 135^0=-\tan 45^0=\dfrac{-\sqrt{2}}{\sqrt{2}}$

therefore,

$z=-\sqrt{2}+\sqrt{2}i$

There may be a better approach.

 

[pasmith]

It should not be necessary to convert from radians to degrees. One should know $$\begin{split} \cos 0 &= \sin \frac \pi 2 = 1 \\ \cos \frac \pi 6 &= \sin \frac \pi 3 = \frac{\sqrt{3}}2 \\ \cos \frac \pi 4 &= \sin \frac \pi 4 = \frac 1{\sqrt{2}} \\ \cos \frac \pi 3 &= \sin \frac \pi 6 = \frac 12 \\ \cos \frac \pi 2 &= \sin 0 = 0 \end{split}$$ These, together with basic identities such as the angle sum and difference formulae, suffice to answer these questions.

 

[Steve4Physics]

$z=2\left[\cos \dfrac{3π}{4} + i \sin \dfrac{3π}{4}\right]$

Expanding gives $z=2\cos (\frac{3π}{4}) + 2 i \sin (\frac{3π}{4})$.

So it’s simply a case of matching the real and imaginary parts:
$x = 2\cos ( \frac{3π}{4})$
$y = 2 \sin ( \frac{3π}{4})$

No need to use ‘$\tan$’. And as already noted by @pasmith, it’s worth getting used to working in radians.

A couple of useful relationships are
$cos(\frac π2 + θ) = - sinθ$ and
$sin(\frac π2 + θ) = cos(θ)$.
For example, using the first relationship tells you $\cos (\frac{3π}{4}) = -sin ( \frac π4)$.