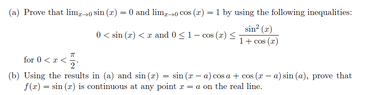Find Limit of cos(x) with Inequalities | Part (b) Help
- Context: MHB
- Thread starter Joe20
- Start date
-
- Tags
- Continuous Proof
Click For Summary
SUMMARY
The discussion focuses on finding the limit of cos(x) as x approaches 0 using inequalities. It establishes that 0 ≤ 1 - cos(x) ≤ sin²(x)/(1 + cos(x)), leading to the conclusion that the limit A must equal 1. For part (b), the transformation u = x - a simplifies the limit evaluation, allowing the use of the sine addition formula to find the limit as u approaches 0.
PREREQUISITES- Understanding of limits in calculus
- Familiarity with trigonometric functions, specifically sine and cosine
- Knowledge of the sine addition formula
- Basic skills in manipulating inequalities
- Study the properties of limits in calculus
- Learn about the sine addition formula in detail
- Explore the application of inequalities in limit proofs
- Investigate the behavior of trigonometric functions near zero
Students studying calculus, particularly those focusing on limits and trigonometric functions, as well as educators seeking to explain these concepts effectively.
Similar threads
Undergrad
Regarding Wirtinger's inequality
- · Replies 4 ·
Undergrad
Inequality from a continuity exercise
- · Replies 9 ·
- · Replies 2 ·
- · Replies 3 ·
- · Replies 3 ·
- · Replies 1 ·
- · Replies 5 ·
- · Replies 8 ·