SUMMARY
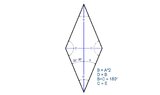
The discussion focuses on calculating the angles of a rhombus given that the angle between the diagonal and a side is 22º30’. The calculations confirm that angle B is 45º, angle D is also 45º, while angles C and E are both 135º. The total interior angles of the rhombus sum up to 360º, consistent with the properties of rhombuses. The method used effectively utilizes the congruency of opposing angles in a rhombus.
PREREQUISITES
- Understanding of basic geometry concepts, particularly properties of rhombuses.
- Knowledge of angle relationships in polygons.
- Familiarity with angle measurement in degrees and minutes.
- Ability to perform basic arithmetic operations with angles.
NEXT STEPS
- Study the properties of parallelograms and their relationship to rhombuses.
- Learn about angle bisectors and their applications in geometric figures.
- Explore the concept of congruence in triangles and quadrilaterals.
- Investigate the use of trigonometric functions in calculating angles in various shapes.
USEFUL FOR
Students studying geometry, educators teaching geometric properties, and anyone interested in understanding the calculations involved in determining angles of rhombuses.