MHB Prove Angle of Diagonals in Quadrilateral is Degrees

[maxkor]

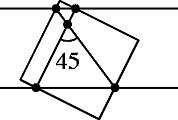
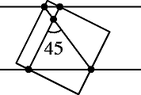
Two angles of a square with side

protrude beyond a strip of width

with parallel edges. The sides of the square intersect the edges of the strip at four points. Prove that the diagonals of the quadrilateral whose vertices are these points intersect at an angle of

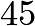degrees.

 

[Opalg]

As in a previous problem, here is an algebraic solution. I would like to see a geometric solution giving more insight into why this result holds.

Spoiler

We may as well take $a=1$. Tilt the diagram so that the square becomes the unit square, and suppose that the parallel lines make an angle $\theta$ with the $x$-axis.

[TIKZ][scale=1.25]
\draw [very thick] (0,0) -- (4,0) -- (4,4) -- (0,4) -- cycle ;
\draw [very thick] (-4,0.5) -- (4,6.5) ;
\draw [very thick] (0,-1.5) -- (8,4.5) ;
\coordinate [label=left:$A$] (A) at (0,3.5) ;
\coordinate [label=above:$B$] (B) at (0.667,4) ;
\coordinate [label=right:$C$] (C) at (4,1.5) ;
\coordinate [label=below:$D$] (D) at (2,0) ;
\draw [very thick] (A) -- (C) ;
\draw [very thick] (B) -- (D) ;
\draw (2.5,0.2) node {$\theta$} ;
\draw (1.3,2.6) node {$\phi$} ;
\draw (-0.5,0) node {$(0,0)$} ;
\draw (4.5,0) node {$(1,0)$} ;
\draw (-0.5,4) node {$(0,1)$} ;
\draw (4.5,4) node {$(1,1)$} ; [/TIKZ]
The equations of the parallel lines are then of the form $y = x\tan\theta + c+d$ and $y = x\tan\theta + c-d$ for some constants $c$ and $d$. The condition that the lines form a strip of width $1$ is $2d\cos\theta = 1$. So $2d = \sec\theta$.

The points where the lines cross the sides of the square are then $$ A = (0,c+d),\qquad B = ((1-c-d)\cot\theta,1), \qquad C = (1,\tan\theta + c-d), \qquad D = ((d-c)\cot\theta,0) .$$ The slope of the line $AC$ is therefore $\tan\theta - 2d = \tan\theta - \sec\theta$.

The slope of $BD$ is $\dfrac{-1}{(2d-1)\cot\theta} = \dfrac{-\tan\theta}{\sec\theta-1}$.

It follows from the formula $\tan(\alpha - \beta) = \frac{\tan\alpha -\tan\beta}{1+ \tan\alpha\tan\beta}$ that if $\phi$ is the angle between $AC$ and $BD$ then $$\begin{aligned} \tan\phi = \frac{(\tan\theta - \sec\theta) - \frac{-\tan\theta}{\sec\theta-1}}{1 + (\tan\theta - \sec\theta) \frac{-\tan\theta}{\sec\theta-1}} &= \frac{(\sec\theta - 1)(\tan\theta - \sec\theta) + \tan\theta}{(\sec\theta - 1) - \tan\theta (\tan\theta - \sec\theta)} \\ &= \frac{\sec\theta(\tan\theta - \sec\theta + 1)}{\sec\theta(1 - \sec\theta + \tan\theta)} \\ &= 1. \end{aligned}$$ It follows that $\phi = 45^\circ$.

 

[maxkor]

Hint

 

[maxkor]

1 / α + β = 90
2 / it is enough to note that the triangles
KNP and MLQ (they have two heights of length "a") so they are isosceles
so |∡NMQ| =90 - α/2 and |∡MNP| =90 - β/2
γ=(α + β)/2=45