Find the volume of the given prism

[chwala]

Homework Statement

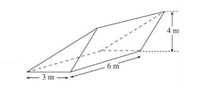
Find the Volume of the given prism

Relevant Equations

base area times height

Find the question below;

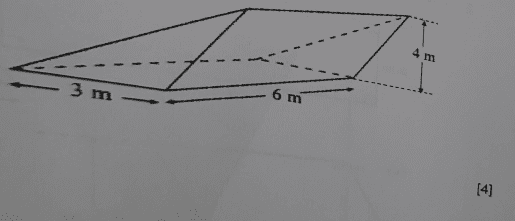
This is a textbook question and i noted that their solution of, $$A=\left[\dfrac{1}{2}×3×4×6\right]cm^3$$ is not correct in my opinion as the base is not a right angle. The base can be analysed as a rhombus and the exercise therefore is to find the related angles and sides (possibly use sine and cosine rules). I would appreciate your thoughts on this.

 

[chwala]

Looks like the text was correct,...I just discussed with a colleague...interesting

 

[sysprog]

You didn't state the conditions that were presumably in the problem statement, but aren't explicit in the diagram, e.g. whether the subfigure with the 6m base is or is not a non-rectangular paralellogram, etc. $-$ what's up with that? Without those conditions, there's no unique solution.

 

[chwala]

You didn't state the conditions that were presumably in the problem statement, but aren't explicit in the diagram, e.g. whether the subfigure with the 6m base is or is not a non-rectangular paralellogram, etc. $-$ what's up with that? Without those conditions, there's no unique solution.

Just amended...was supposed to be volume and not area.

 

[Lnewqban]

Just amended...was supposed to be volume and not area.

... and cubic meters rather than cubic centimeters.

 

[sysprog]

Just amended...was supposed to be volume and not area.

That's not the point $-$ you didn't post any of the parameters of the question. Please consider the following modified version of your diagram:

In this diagram, the area or volume of the figure with lines A', B' and C' is gretaer than that of the figure with lines A, B, and C. There is no way to know what the area of volume of the figure is,becuase no information is given that rules out such a substitution.

You did the same thing earlier this month with this post
(https://www.physicsforums.com/threads/find-the-area-of-the-quadrilateral.1011088/):

The problem with that was well explained to you, and you have just done exactly the same thing again.

Please try to learn from the cogent answers that you are given.

 

[chwala]

That's not the point $-$ you didn't post any of the parameters of the question. Please consider the following modified version of your diagram:

View attachment 295939

In this diagram, the area or volume of the figure with lines A', B' and C' is gretaer than that of the figure with lines A, B, and C. There is no way to know what the area of volume of the figure is,becuase no information is given that rules out such a substitution.

You did the same thing earlier this month with this post
(https://www.physicsforums.com/threads/find-the-area-of-the-quadrilateral.1011088/):

View attachment 295940

The problem with that was well explained to you, and you have just done exactly the same thing again.

Please try to learn from the cogent answers that you are given.

Noted I guess I have to be careful with the questions...

 

[chwala]

I think it would be ideal for me to post the problem as it appears on the text then we would be able to have a clearer picture...

our interest in on part (b).
Generally for prisms;
Volume= base area times height.
for part (a), its straightforward,$V=\dfrac {1}{2}×2⋅5×7×12=210cm^3$
it also follows that for part (b),
$V=\dfrac {1}{2}×3×4×6=36m^3$...this was a bit confusing because of the base area which is not a right angle triangle but someone pointed out to me that i could use the height given and use the base of $3$metres given on the problem... then it clicked.

 

[sysprog]

There must be more than that in the text. For example, somewhere in the text there must be a reference to the diagram label "[4]". Please quote the entirety of the text in which reference to the diagram is made.

In a reply that apparently you posted and then edited out, you said:

there were no conditions, this is an O- level textbook problem and I indicated the question as it is on the textbook...

Is it a multiple-choice question? If so, then the associated restriction on possible answers, along with a rule to choose the best answer if none of the choices is certain, should be construed as part of the question. Please post the whole question.

 

[chwala]

That is the whole question in the worksheet questions...this is how the particular page looks like...just a set of questions and no point of reference...

 

[chwala]

There must be more than that in the text. For example, somewhere in the text there must be a reference to the diagram label "[4]". Please quote the entirety of the text in which reference to the diagram is made.

In a reply that apparently you posted and then edited out, you said:
Is it a multiple-choice question? If so, then the associated restriction on possible answers, along with a rule to choose the best answer if none of the choices is certain, should be construed as part of the question. Please post the whole question.

The [4] that you are referring to is the marks allocated for part (a) and (b)...this is not a multiple choice question, the question is as it is...and i have indicated how i approached it...unless you are of the opinion that the question in itself is not sufficient ...but i guess going with part (a) of the problem, then finding volume for part (b) should not be a big task...it would follow from (a)...

 

[sysprog]

Please quote any text that introduces any conditions common to the set of worksheet questions.

 

[chwala]

I am not getting you...is the question wrongly stated/framed? or is your concern on my use of the term "text"? A textbook covering the chapter of Area, Perimeter and Volume would have worksheet questions at the end of the chapter...isn't that so?

 

[DaveC426913]

I can't see any shortcoming in the question.
It's a prism with dimensions 3x4x6.
Frankly, that seems all you need to know to solve it.
You don't even need to know which measurement is the altitude.
½x3x4x6 is the same as 3x½x4/6.

 

[sysprog]

My concern is that the information that you've given is insufficient to allow a unique answer to the question. I think that there must be something somewhere in the body of the text that indicates e.g. that the 'top line' in (a) is also 12cm long or that the dotted vertical line is also 7cm long.

 

[DaveC426913]

My concern is that the information that you've given is insufficient to allow a unique answer to the question. I think that there must be something somewhere in the body of the text that indicates e.g. that the 'top line' in (a) is also 12cm long or that the dotted vertical line is also 7cm long.

Post #10:

"4. Calculate the volume of each of the following prisms:"

 

[sysprog]

I can't see any shortcoming in the question.
It's a prism with dimensions 3x4x6.
Frankly, that seems all you need to know to solve it.
You don't even need to know which measurement is the altitude.
½x3x4x6 is the same as 3x½x4/6.

Thanks, @DaveC426913, I abjectly stand corrected, with apologies to @chwala $-$ I somehow forgot the definition of prism.

 

[chwala]

Thanks, @DaveC426913, I abjectly stand corrected, with apologies to @chwala $-$ I forgot the definition of prism.

No worries...thanks for your time on this...I also learned something new today...cheers.

 

[chwala]

The question was quite tricky yet very easy if one knows the formulae for finding volume of prisms. I would like to ask if we can use a different approach in finding the volume of this prism by noting that the height is $4m$ but not necessarily using the height directly. I am thinking of the base in this terms; if i extend the lines as shown, then we have a rhombus...i think at the end one can work out on finding the 3 dimensions of the triangle and use heron's formula...

 

[DaveC426913]

The question was quite tricky yet very easy if one knows the formulae for finding Volume of prisms. I would like to ask if we can use a different approach in finding the volume of this prism by noting that the height is $4m$ but not necessarily using the height directly. I am thinking of the base in this terms; if i extend the lines as shown, then we have a rhombus...i think at the end one can work out on finding the 3 dimensions of the triangle and use heron's formula...

Indeed. I haven't dealt with prisms since high school but ... as soon as we wrote out the equation:
1/2x3x4x6, I realized that it didn't matter which measurement was the altitude; they all worked out to the same volume - half of the rhomboid formed by duplicating the prism.

 

[chwala]

Will the area of the triangle on the base area be equal to area of half of the rhomboid? I doubt that...

 

[sysprog]

I think that you know that it's not $-$ base times height of a rhomboid equals its area, and half of base times height of a triangle equals its area, so the area of the 3m base 4m height triangle is only one quarter of that of the 6m base 4m height rhomboid.

 

[DaveC426913]

I think that you know that it's not $-$ base times height of a rhomboid equals its area, and half of base times height of a triangle equals its area, so the area of the 3m base 4m height triangle is only one quarter of that of the 6m base 4m height rhomboid.

What?

The face that is 6m x 4m is a rectangle , not a rhomboid. The prism is a 3 dimensional object. We're seeing a 4x6 rectangle at an oblique angle. The face that is 3m x 4m(alt) is a triangle whose area is half that of a rhomboid of the same dimensions.

 

[sysprog]

That's twice in the same thread @DaveC426913 $-$ of course you're right again $-$ thanks for your vigilance.

 

[chwala]

What?

The face that is 6m x 4m is a rectangle , not a rhomboid. The prism is a 3 dimensional object. We're seeing a 4x6 rectangle at an oblique angle.The face that is 3m x 4m(alt) is a triangle whose area is half that of a rhomboid of the same dimensions.

Yes, this is correct...cheers Dave

 

[chwala]

What?

The face that is 6m x 4m is a rectangle , not a rhomboid. The prism is a 3 dimensional object. We're seeing a 4x6 rectangle at an oblique angle.The face that is 3m x 4m(alt) is a triangle whose area is half that of a rhomboid of the same dimensions.

Going with post $19$, out of curiosity, then what would be the dimensions of the rhombus?...yes, I can see the $6$ by $4$ rectangle...this part is clear.

 

[DaveC426913]

Going with post $19$, out of curiosity, then what would be the dimensions of the rhombus?

Base 3, height 4. Area = exactly double the triangle.

 

[chwala]

Base 3, height 4. Area = exactly double the triangle.

Consider my diagram in post $19$, are we having a rhombus or a rectangle? i just want to ascertain the dimensions, one dimension is already given i.e $w=3$metres. What is the other dimension? $w$ by $w$ in case of rhombus or $w$ by $l$ in case of rectangle. We already have $w=3$metres. I hope you understand my question.

I will work backwards, the cross-sectional area (of the triangle) is equal to $6m^2$ Since you mentioned that this is a half of the cross-sectional area...(i will assume that the cross-section is either a rhombus or a rectangle), it follows that our cross-sectional area is equal to $12m^2$ implying that we are having a rectangle of dimensions $3 ×4$ metres. .. which is again highly unlikely because the height of the triangle is also equal to $4$m.

I will look into finding the dimensions of the triangle again...the unknown dimension ought to be more than $4$m...using pythagoras theorem.

 

[DaveC426913]

Consider my diagram in post $19$, are we having a rhombus or a rectangle?

I have labeled the diagram here.

You are talking about abcd.

It could be a rectangle - though it sure doesn't look like one. It could also be a rhombus, though that is unlikely too. A rhombus has four equal-length sides. We would need to know that ab is the same length as bc, and we have no reason to assume that.

All we really know is that it's a parallelogram (because we constructed it to have parallel sides).

But it's actually irrelevant which one it is; they all use the same formula: bxh.

(i will assume that the cross-section is either a rhombus or a rectangle)

You cannot assume this. Though, again, its actual sub-shape doesn't come into play in this case.

 

[DaveC426913]

I will look into finding the dimensions of the triangle again...the unknown dimension ought to be more than $4$m...using pythagoras theorem.

You are not given enough information to figure out the length of ac.
The only thing you can say about it is that it must be at least length 5.
(That would form a 3-4-5 right triangle - the smallest it can be)
But its upper limit is unbounded - and cannot be derived with the given information.

 

[chwala]

I have labeled the diagram here.

View attachment 296049
You are talking about abcd.

It could be a rectangle - though it sure doesn't look like one. It could also be a rhombus, though that is unlikely too. A rhombus has four equal-length sides. We would need to know that ab is the same length as bc, and we have no reason to assume that.

All we really know is that it's a parallelogram (because we constructed it to have parallel sides).

But it's actually irrelevant which one it is; they all use the same formula: bxh.You cannot assume this. Though, again, its actual sub-shape doesn't come into play in this case.

Thanks Dave, noted ...cheers