hilton
- 2
- 0
- Homework Statement
- Consider the motion of a particle in a potential: x`` = −U`(x). Can this equation also describe the arclength parameter of a bead sliding under gravity on an appropriately shaped wire? That is, find the curve y = V (x) such that the arc length parameter s of a bead sliding on this curve under
gravity (g = const. pointing down the y-axis) satisfies the same equation: s`` = −U`(s), and state under what conditions on U this is possible. Find V in the following two cases: (i) U = x^2/2 and (ii) U = −cos x.
- Relevant Equations
- Serret-Frenet Triad, F=ma
For the case first case U=x^2/2 :
1) Find the Serret-Frenet Triad for a any curve y = f(x):
For a curve on a plane, the Triad could be find in this way:
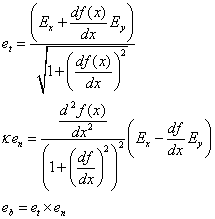
2) The vector force resultant acting in the bead could be discribed in this way:
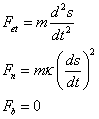
3) The vector force acting in the bead could be discribed in this way:
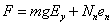
4) Multypling (3) with (1) and equalizing to (2):
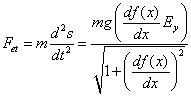
5) From the question, we know that (4) is equal to -U`(s), so solving the differential equation, we have:
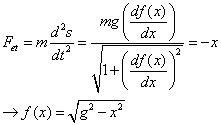
6) But the answer is a cycloid , so there is somethig wrong.
1) Find the Serret-Frenet Triad for a any curve y = f(x):
For a curve on a plane, the Triad could be find in this way:
2) The vector force resultant acting in the bead could be discribed in this way:
3) The vector force acting in the bead could be discribed in this way:
4) Multypling (3) with (1) and equalizing to (2):
5) From the question, we know that (4) is equal to -U`(s), so solving the differential equation, we have:
6) But the answer is a cycloid , so there is somethig wrong.