Find speed of the racing car as it crosses finish line - Mechanics

[chwala]

Homework Statement

See attached ( reference is example 1.4.1)

Relevant Equations

$s=ut$

This is a textbook problem (Mechanics).
Attached find the question and respective solution.

This is fine with me, i like trying different ways of solving math related problems. My approach is as shown below.

Using the graph sketch

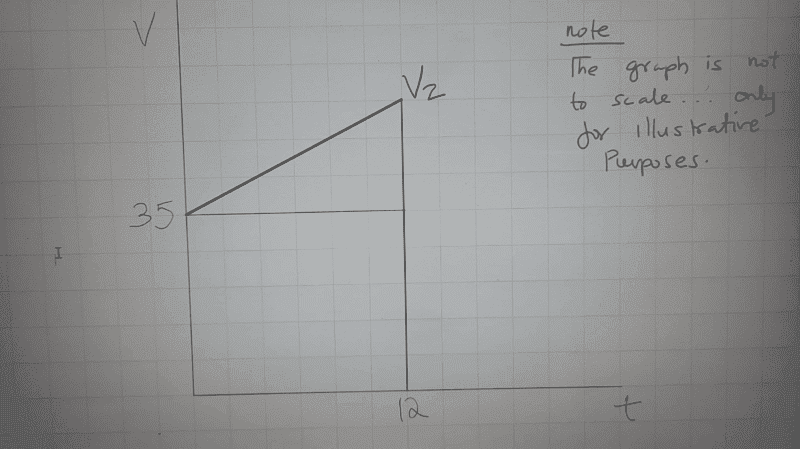
It follows that,
$s$= $(35×12)$+$\frac {1}{2}$×$12(v_2 -35)$
$600= 420+6(v_2-35)$
$600 = 420 + 6v_2-210$
$600 = 210 + 6v_2$
$390 = 6v_2$
→$v_2 = 65$ m/s bingo

Any other approach will be appreciated...

 

[BvU]

It follows that,
$s$= $(35×12)$+$\frac {1}{2}$×$12(v_2 -35)$
...
Any other approach will be appreciated...

You have of course noticed that you are solving the exact same equation...

For those of us for whom it is a sport to memorize a minimum of stuff, the $s = {1\over 2} (u+v) t$ requires derivation, which is work. Remembering $s = v_0t+\frac 1 2 at^2$ is somehow burnt into our brain and then it becomes a two step process:$$600 \ {\mathsf m} = 35*12 \ {\mathsf m} + \frac 1 2 at^2 \quad\Rightarrow\quad a = \frac {360} {144}$$ $$u = v_0 + at \quad\Rightarrow\quad u = 35 \ {\mathsf m/s} + \frac {360} {12} \ {\mathsf m/s} $$
And here we are $-$ of course $-$ solving the same equation, whether this is actually an other approach is a matter of taste...

$\$

 

[chwala]

nice ...yes its true that one has to get the derived term i.e $s$=$\frac {1}{2}$$(u+v)t$ from
$s$= $ut$+$\frac {1}{2}$$at^2$...(1)
and $v=u +at$, .....(2)
from (2)
$→at=v-u$
$→a$=$(\frac {v-u}{t})$...(3)
Now, substituting (3) into (1) we get,
$s$= $ut$+$\frac {1}{2}$$(\frac {v-u}{t})$$t^2$
$s$= $ut$+$\frac {vt^2-ut^2}{2t}$
$s$= $\frac {2t^2u+vt^2-ut^2}{2t}$
$s$= $\frac {ut^2+vt^2}{2t}$
$s$=$\frac {t}{t}$× $(\frac {ut+vt}{2})$
$→s$=$\frac {1}{2}$$(u+v)t$ as required in the problem...