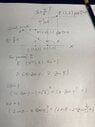Find the angular velocity of this linkage

[Noob of the Maths]

Homework Statement

If the angular velocity of link AB is w(AB)=4 rad/s at the instant shown, determine the velocity of the sliding block E at that instant. Also, identify the type of motion of each of the four links.

Relevant Equations

V = w(r)

Hi! everyone! ;)

I have a problem with the development of this problem.

I need to resolve it with 2 procedures: trigonometry and instant centers. My advance can be see in the next image:

The instant centers procediment its (1) up and trigonometry procediment its (2) down.

I know that the result its 4 rads/s. But in my answer its not make the sense ;( and i don't know why the angular velocity of "D" its 4 rads/s.

PD: I don't can use cross product for resolve it... only trigonometry and instant centers (separately).

Thanks for read ;)

 

[anuttarasammyak]

I would introduce xy coordinate as sketched.
From these linear equations for sin$\phi$ and cos$\phi$ we can delete $\phi$ and get x, the horizontal coordinate of E, as function of $\theta$ which is function of time.

[EDIT] The formula are written as
$$(x/2-\cos\phi-\beta)^2+(1-\sin\phi)^2=1/4$$
$$(x/2-\cos\phi-\cos\theta)^2+(1-\sin\phi-\sin \theta)^2=1/4$$
where
$$\beta=\frac{\sqrt{3}-1}{2}=\frac{1}{\sqrt{3}+1}$$
Solving this equation for sin$\phi$ and cos$\phi$ and using the relation
$$\sin^2\phi+\cos^2\phi=1$$
The relation of x and $\theta$ is given as
$$(b_1c_2-b_2c_1)^2+(c_1a_2-c_2a_1)^2=(a_1b_2-a_2b_1)^2...(1)$$
where
$$a_1=1$$
$$a_2=1-\sin\theta$$
$$b_1=\frac{x}{2}+\frac{\sqrt{3}-1}{2}$$
$$b_2=\frac{x}{2}-\cos\theta$$
$$c_1=\frac{3}{8}+\frac{a_1^2+b_1^2}{2}$$
$$c_2=\frac{3}{8}+\frac{a_2^2+b_2^2}{2}$$
Differentiating (1) by t for t=0 we would know $\dot{x}(t=0)$. After calculation I got
$$\dot{x}=-3.017 r\dot{\theta}$$ for initial time t=0, where r is 1 length unit for rods. I do not have trust of my calculation. I should appreciate it if someone would challenge it too.

 

[Noob of the Maths]

I would introduce xy coordinate as sketched.
From these linear equations for sin$\phi$ and cos$\phi$ we can delete $\phi$ and get x, the horizontal coordinate of E, as function of $\theta$ which is function of time.

yep, i can use a free body diagram, but in this pariticulary case i only can use the procedure as I put it. The most important are the traslation and rotation diagram and the use of angles in triangles.

 

[Master1022]

yep, i can use a free body diagram, but in this pariticulary case i only can use the procedure as I put it. The most important are the traslation and rotation diagram and the use of angles in triangles.

Hi, I think you should put this into the engineering forum. Does your method allow for sketching velocity diagrams?

 

[Noob of the Maths]

Hi, I think you should put this into the engineering forum. Does your method allow for sketching velocity diagrams?

Yes, velocity diagrams its allowed. Hi :)

 

[Master1022]

Yes, velocity diagrams its allowed. Hi :)

Cool, so the steps I would think about when going down the velocity diagram route are:
1. A and C are fixed
2. E is constrained to pure horizontal movement, as is D (in this case) as CD is vertical
3. We know $\omega_{AB}$ and thus know where point B is
4. To get from point B to point D, we then know there must be a rotation between the two
5. Then to get from D to E, given that E is constrained to horizontal movement, it suggests to me that $\omega_{DE} = 0$ at this instant. However, you said that the answer is $\omega_{DE} = 4$ rad/s, or did I misunderstand what you said?

I hope this rough outline makes sense. I can try to make a sketch a bit later

 

[Noob of the Maths]

Cool, so the steps I would think about when going down the velocity diagram route are:
1. A and C are fixed
2. E is constrained to pure horizontal movement, as is D (in this case) as CD is vertical
3. We know $\omega_{AB}$ and thus know where point B is
4. To get from point B to point D, we then know there must be a rotation between the two
5. Then to get from D to E, given that E is constrained to horizontal movement, it suggests to me that $\omega_{DE} = 0$ at this instant. However, you said that the answer is $\omega_{DE} = 4$ rad/s, or did I misunderstand what you said?

I hope this rough outline makes sense. I can try to make a sketch a bit later

This very helpful!, i know that my mistakes its in the diagram and their angles. wDE= 4 rad/s based on assumptions,

 

[Lnewqban]

Consider that:
1) E can only have horizontal movement.
2) Only the horizontal component of the instantaneous velocity of D has influence on E.
3) Because both are connected by a horizontal link, the horizontal components of the instantaneous velocity of D and B must be equal.
4) Since you are given the angular velocity of the 2 feet long link AB, you can calculate the tangential velocity of B and then, its instantaneous horizontal component.

 

[haruspex]

I should appreciate it if someone would challenge it too.

You are way overthinking it.
It is really quite simple following @Lnewqban's scheme.