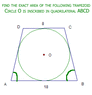
Find the area of trapezoid circumscribed about a circle?

[Yuki]

Hello, I have encounted this problem and really need some help =/
The figure is attached. Or you can view it in here: http://img404.imageshack.us/img404/1120/mathhelpppp6yk.gif"

Thanks a lot, really urgent

 

[robphy]

What figures can you compute the area of?
Can you find those figures in this diagram? (Remember, area is additive.)
How would you use information about the circle?

 

[Yuki]

I have tried to create a rectangle inside that trapezoid, which is from point D and C down to the bottom line. Even though so =s I still can't keep moving =s I note the angle thing on the trapezoid. But like, I also tried to see if I can figure out the degree of Angle CBA or DAB Yet I still get stucked =( I don't know what I am missing to move to next step =/
Thanks for the fast reply

 

[robphy]

Can you find the area of a triangle?
Do you know the relationship between a radius and a tangent?

 

[Yuki]

I know how to find the area of a triangle. However, many triangles can be formed in there =/ So I am kinda lost =s I know radius and tangent, however I never learned any relationship between raidus and tangent
Thanks a lot for help!

 

[robphy]

If you can break up your figure into triangles, and you can find the areas of those triangles, then you can add these areas to get the area of the whole figure.

Do you know that at any point on the circle, the radius and tangent-line are perpendicular?

 

[0rthodontist]

Here is a hint:

If two line segments share a common endpoint p, and are each tangent to a circle at their opposite endpoints, they have the same length.