BvU
Science Advisor
Homework Helper
- 16,219
- 4,933
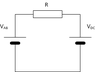
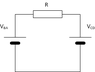
Going round the loop, emf = VAB+VCD = VAB-VDCHelly123 said:What makes the sign different? Since, B, v still the same?
Do the math and post...And where the 'b' comes from the options?
The free charge carriers in the wire can move under the influence of the force. The Lorentz force is the underlying phenomenon. It's extremely important in physics. As to the 'why?' of the Lorentz force: you can dig deeper into the fundamentals of electrodynamics, but a 'why?'question is ultimately not answerable. Physicists restrain themselves and search for the 'how?'.Helly123 said:What makes the wire have magnetic force?
It did not. It only said you don't have to take into account the magnetic field due to the current in the loop. The whole exercise can also be done by determining the magnetic flux through the loop (the flux due to ##I## in the long wire ) and applying Faraday's law.Why the question said that the magnetic flux density is negligible?