- #1
Eclair_de_XII
- 1,083
- 91
Homework Statement
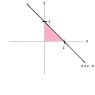
"Given that the joint distribution of ##X## and ##Y## is ##f(x,y)=\frac{1}{2}(x+y)e^{-(x+y)},\text { for } x,y>0## and ##0## otherwise, find the distribution of ##Z=X+Y##."
Homework Equations
##f_Z(z)=\int_{\mathbb{R}}f(x,z-x)dx##
##P(Z<z)=F_Z(z)=P(X+Y<z)=P(Y<z-X)=\int_{\mathbb{R}} \int_{-\infty}^{z-x}f(x,y)dydx##
The Attempt at a Solution
##f_Z(z)=\int_0^\infty \frac{1}{2}[x+(z-x)]e^{-[x+(z-x)]}dx=\frac{1}{2} \int_0^\infty ze^{-z}dx=\frac{1}{2}ze^{-z}x|_0^\infty##
The problem is that the density function seems to always tend towards infinity no matter which equation I use...
Last edited: