Find the distance CD in the given complex variable question

[chwala]

Homework Statement

See attached

Relevant Equations

complex variables

This is the problem;

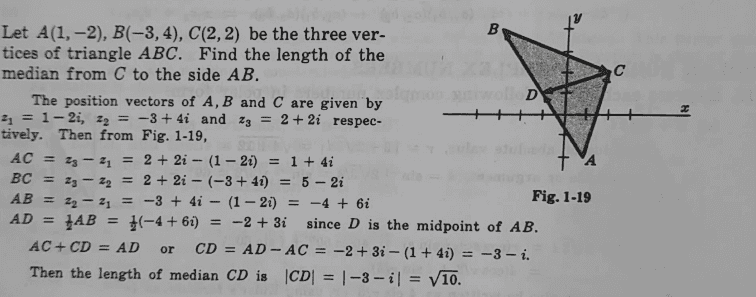
Note that i am conversant with the above steps shown in the solution, having said that i realized that we could also borrow from the understanding of gradient and straight lines in finding the distance $CD$... it follows that the equation of $BA= -1.5x-0.5$, implying that the co ordinates of $D(x,y) = (2-3, 4-3) = (-1,1)$ and using the distance formula, it follows that;
$CD= √[(3)^2 + (1)^2]$= $√10$ as indicated...

any other approach guys...

 

[anuttarasammyak]

$$\vec{OD}=\frac{1}{2}(\vec{OA}+\vec{OB})=\frac{1}{2}(1-3,-2+4)=(-1,1)$$
$$\vec{DC}=(2-(-1),2-1)=(3,1)$$

 

[FactChecker]

Keeping in mind that the point of the exercise might be for you to get more comfortable with complex numbers, I hope that you are comfortable with their solution. There are often multiple ways to get the same, true, answer. Some are easier than others. You may soon see examples where the use of complex numbers makes solutions much easier.

 

[chwala]

True, the whole idea is to have an understanding of the argand diagram and also the Complex number, say $Z = x + iy$, then it follows that the Modulus of
$Z =|x+ iy|= √[(x^2 +y^2)]$, and also a good understanding of vectors is required.

---

---

 

[chwala]

...but looking at this problem, we could also just use the relationship of $AD= \frac {1}{2}AB$.
letting the co ordinates of point $D$ be $(x,y)$, then $AB= (-3-1)+i(4+2)$
$AB= -4+6i$, therefore $AD= -2+3i$, also to find the co ordinate of $AD= (x-1=-2, y+2=3)$
giving us the co ordinates, $(-1,1)$
$CD= (-1-2)+ (1-2)i= -3-i$