NotInMrPutmansClass
- 5
- 0
- Homework Statement
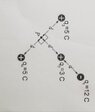
- Calculate the net electric field at point P from the diagram below
- Relevant Equations
- E=(kq)/r^2
Where k is plank's constant 9×10^9
R= distance or radius
Since q3=q4 and they are opposite to each others they cancel out
But as soon as I try to find the electric field of one of the charges, I need the radius which is not given.
By isolating the electric field for radius
E=(kq)/r^2
I now have two unknowns
But as soon as I try to find the electric field of one of the charges, I need the radius which is not given.
By isolating the electric field for radius
E=(kq)/r^2
I now have two unknowns