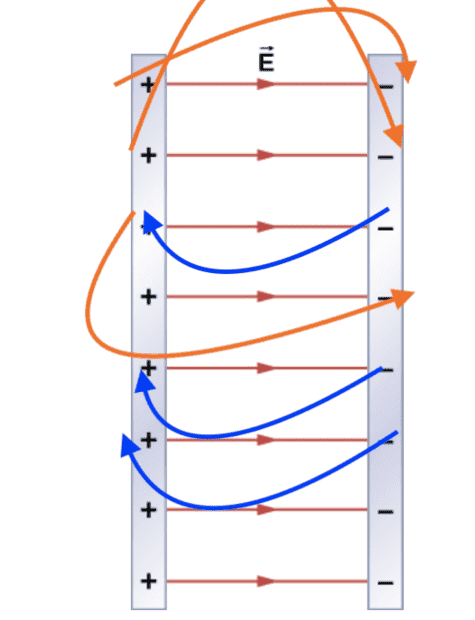
The electric field resulting from two infinite planes, one positive and one negative, exhibits distinct behavior as described by Gauss's law. The electric field lines from the positive plane point away from it, while those from the negative plane point towards it, creating a scenario where they amplify each other between the plates rather than canceling out. This results in a uniform electric field in the region between the plates, while outside the plates, the fields cancel each other. Understanding this concept is crucial for analyzing electric fields in electrostatics.
PREREQUISITESStudents of physics, educators teaching electrostatics, and professionals in electrical engineering seeking to deepen their understanding of electric fields and their interactions.
Electric field lines originate at positive charges and stop at negative charges. That follows from Gauss's law. You can draw the blue lines if you wish, but you have to be careful. Remember that the electric field points in the direction of the force on a positive test charge. A positive test charge placed between the plates will experience a repulsive force from the positive charges on the left and an attractive force from the negative charges on the right. So if you draw blue lines representing the electric field from the negative charges, they should point left to right, same as the red lines. In that case you might as well draw one set of lines and be done with it.annamal said: