Ronka
- 7
- 0
Find the equation for Sine and cosine from a graph
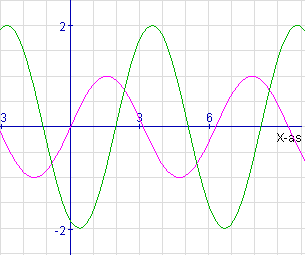
Hello people, i have had a little problem solving this graph. It looks really easy, but I am still couldn't solve it ?!
a x Sin (bx + c) + d
a = amplitude
b = period
c = phase shift
d = vertical shift
thx in advances.
Edit:
I have solved the equation for the Sine ( thank you folks )
Equation for Sine:
2 sin(1(x-2))
Trying to find the equation for Cosine:
Homework Statement
The Attempt at a Solution
Hello people, i have had a little problem solving this graph. It looks really easy, but I am still couldn't solve it ?!
a x Sin (bx + c) + d
a = amplitude
b = period
c = phase shift
d = vertical shift
thx in advances.
Edit:
I have solved the equation for the Sine ( thank you folks )
Equation for Sine:
2 sin(1(x-2))
Trying to find the equation for Cosine:
Last edited: