chwala
Gold Member
- 2,827
- 415
- Homework Statement
- Sketch the region that satisfies the inequalities ##|z|≤3## and ##Im z≥2##
hence find the greatest value of arg ##z## for points in this region in radians.
- Relevant Equations
- complex numbers
since ##|z|≤3## →##z=0+0i##, therefore we shall have centre##(0,0)## and radius ##3##,
find my sketch below,
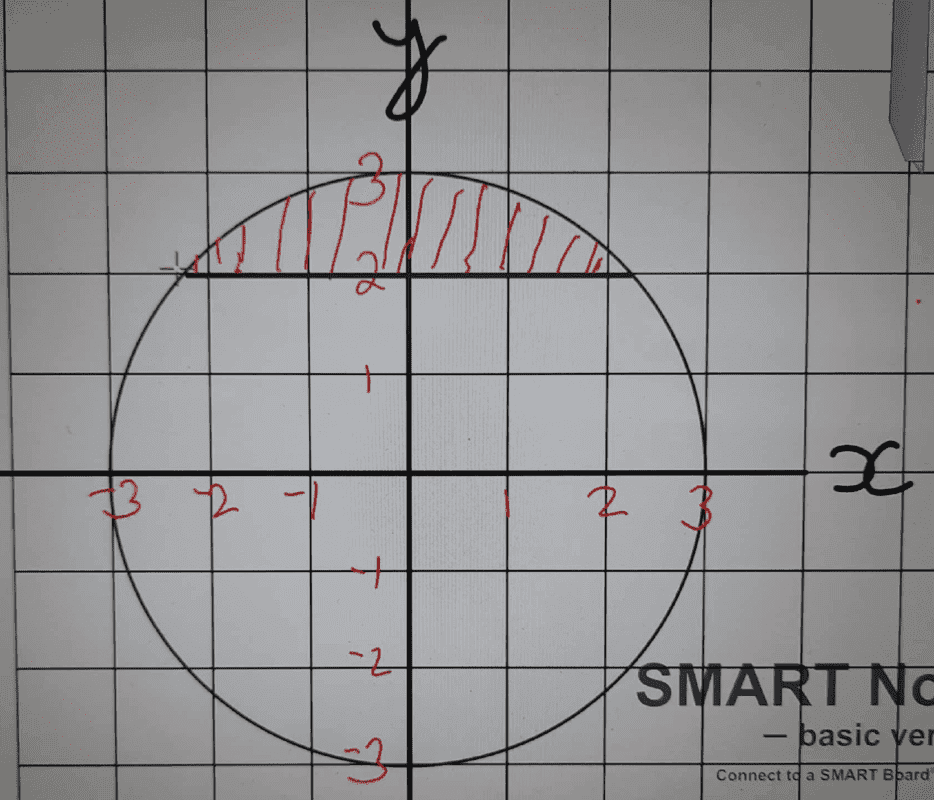
find my sketch below,