- #1
chwala
Gold Member
- 2,656
- 351
- Homework Statement
- See attached.
- Relevant Equations
- Complex numbers
Find the question below; note that no solution is provided for this question.

My approach;
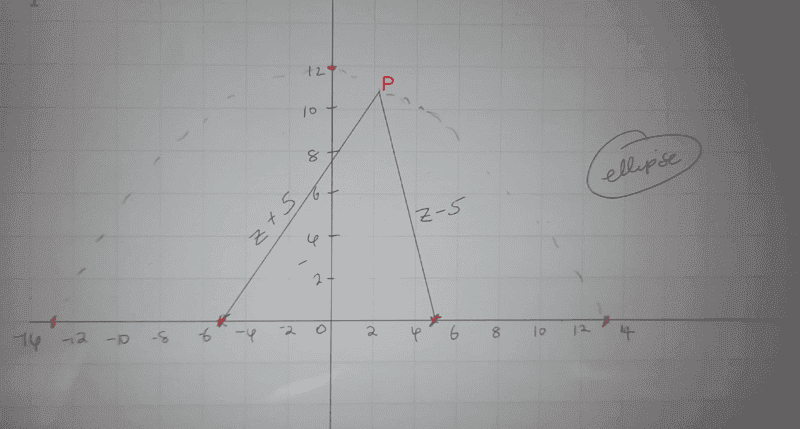
Find part of my sketch here;
* My diagram may not be accurate..i just noted that, ##OP## takes smallest value of ##12## when ##|z+5|=|z-5|## i.e at the end of its minor axis and greatest value ##13## at end of its major axis
We have been given,
##|z-5|+(z+5|=26##
Then ##OP=|z|=|\dfrac{1}{2}((z+5)+(z-5))|##
##≤ \dfrac{1}{2}(|z+5|+|z-5|)=\dfrac{1}{2}×26=13##
Also,
##(|z+5|+|z-5|)^2=676## and ##(|z+5|-|z-5|)^2≥0##, adding this two gives us
##2|z+5|^2+2|z-5|^2≥676##
##⇒|z+5|^2+|z-5|^2≥338##
##(z+5)(z^*+5^*)+(z-5)(z^*-5^*)≥338##
##2zz^*+50≥338##
##2zz^*≥288##
##zz^*≥144##, which is ##|z|^2≥144##
##⇒z≥12##, therefore ##12≤OP≤13##
My approach;
Find part of my sketch here;
* My diagram may not be accurate..i just noted that, ##OP## takes smallest value of ##12## when ##|z+5|=|z-5|## i.e at the end of its minor axis and greatest value ##13## at end of its major axis
We have been given,
##|z-5|+(z+5|=26##
Then ##OP=|z|=|\dfrac{1}{2}((z+5)+(z-5))|##
##≤ \dfrac{1}{2}(|z+5|+|z-5|)=\dfrac{1}{2}×26=13##
Also,
##(|z+5|+|z-5|)^2=676## and ##(|z+5|-|z-5|)^2≥0##, adding this two gives us
##2|z+5|^2+2|z-5|^2≥676##
##⇒|z+5|^2+|z-5|^2≥338##
##(z+5)(z^*+5^*)+(z-5)(z^*-5^*)≥338##
##2zz^*+50≥338##
##2zz^*≥288##
##zz^*≥144##, which is ##|z|^2≥144##
##⇒z≥12##, therefore ##12≤OP≤13##
Last edited: