Find the height of a lamp based on the velocities of projectiles

[stabby_faris]

Homework Statement

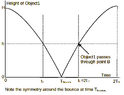
Two small objects are launched horizontally from the same spot A, located at the height H = 4.0 m above horizontal flat surface. Initial velocities of the objects v1 and v2, with v2= 2 v1. Both projectiles hit a lamp B located at the height h from the ground. Calculate distance h to the lamp, assuming that one of the balls bounces a single time from the horizontal surface after perfectly elastic collision. Friction with air can be neglected.

Relevant Equations

s = ut + (1/2)gt^2
v = s/t
Ek = 1/2 * mv^2
Egrav = mgh

Wild question. Even Chat GPT struggling.
What I first attempted was to find the velocity by which the projectile with v1 falls down to the ground with. This part was easy.
Kinetic energy gained = gravitational potential energy lost

Let's define our coordinate frame as up vectors being positive and vectors to the right to be positive as well (like a normal y-x graph)

Since:
(1/2)(mv^2) = mgh then
v = sqrt(2gh) where h = 4 so v = sqrt(8g).

Now we can get the relationship between the time by which the first and second projectile reach the same horizontal displacement.
v = s/t so since the horizontal displacement is the same so:
v1 * t1 = 2v1 * t2
t1 = 2t2

Where t1 is the time taken for projectile with v1 and t2 is the time taken for the projectile with v2
Now let's look at an approach to find t2

let's define the time by which projectile with v1 falls to the ground by "tfall"
and let's define the time by which projectile with v1 rises to height h to lamp by "trise"

-4 = (1/2)(-g)(tfall)^2
so tfall = sqrt(8/g)

Now this is the part where I am struggling

We can think of trise to be associated with: (sqrt(8/g) + trise) = 2t2 where

-(4-h) = sqrt(8g)t2 + (1/2)(-g)(t2)^2 to find t2 as well. Remember, we got sqrt(8g) from the velocity by which it hits the ground when falling in the y direction and it got rebounded with equal speed as it was elastic.
but now it's getting ridiculous and tiring to solve the very algebra of it and I am not even sure if it is correct.

Am I even on the right track? I am not sure how to move on from here.



P.S: This is a physics olympiad training camp question to patten me up

 

[stabby_faris]

A diagram to help out as well

 

[PeroK]

Okay, it took me a few seconds to figure out what they are asking. I think that the projectile with velocity $\vec v_2$ hits the lamp directly. And, the projecile with velocity $\vec v_1$ hits the lamp after first bouncing on the ground.

 

[PeroK]

What about considering a reference frame moving to the right at speed $v_1$?

 

[Orodruin]

For the record: ChatGPT is not a reliable source for solving physics problems.

 

[haruspex]

Consider, if the faster projectile takes time t:

• where is the other at time t?
• when will it hit the ground?
• how do these times relate to h and H?

 

[kuruman]

but now it's getting ridiculous and tiring to solve the very algebra of it and I am not even sure if it is correct.

Take a step back from the problem and think what you have here. Because of the initial horizontal velocities, this is really a 1D free fall problem. Imagine looking at the shadows of the two objects projected on a vertical wall.
Shadow 2 drops down from A to B in time $t_2.$
Shadow 1 drops down from A to the floor and then back up to B in time $t_1.$
Let $T_{\text{AA}}$ be the time it takes for shadow 1 to make the round trip from A back to A. Because $T_{\text{AB}}=T_{\text{BA}}$, it follows that
$t_2=T_{\text{AA}}-t_1$. That's one relation between $t_1$ and $t_2$. You need to look at what's happening in the horizontal direction to find a second relation and then put the two together to find $h$. What do you think that relation looks like?

 

[stabby_faris]

Edit: Very sorry for the late reply, this week drained me but I was actively reading all of your comments

Thank you all for your replies

After using your retrospective questions and hints, and a lot of algebra I still had to muster through...

I got the height as h = 2.5m roughly. Is this correct? Because of the quadratic within the kinematic equations I got 2 results where one height was negative and so was obviously not correct as h is scalar. Looking roughly through the image it satisfies the dimensions even if it is not to scale.

But yeah, the very algebra of it was tiring and frankly annoying to work through, do anyone of you have tips on that?

 

[PeroK]

Edit: Very sorry for the late reply, this week drained me but I was actively reading all of your comments

Thank you all for your replies

After using your retrospective questions and hints, and a lot of algebra I still had to muster through...

I got the height as h = 2.5m roughly. Is this correct? Because of the quadratic within the kinematic equations I got 2 results where one height was negative and so was obviously not correct as h is scalar. Looking roughly through the image it satisfies the dimensions even if it is not to scale.

But yeah, the very algebra of it was tiring and frankly annoying to work through, do anyone of you have tips on that?

I got a rational ratio for $h/H$.

 

[stabby_faris]

I got a rational ratio for $h/H$.

So after substituting values from the equation I am wrong or was this a tip to make the algebra easier than to just substitute immediately?

 

[PeroK]

So after substituting values from the equation I am wrong or was this a tip to make the algebra easier than to just substitute immediately?

If you got $2.5m$, then $h/H = 5/8$. I didn't get that. Although perhaps I made a mistake. The algebra wasn't too bad. Although, plugging and chugging is probably not the way to go at this level.

 

[stabby_faris]

If you got $2.5m$, then $h/H = 5/8$. I didn't get that. Although perhaps I made a mistake. The algebra wasn't too bad. Although, plugging and chugging is probably not the way to go at this level.

Rahh but I love plugging and chugging

Anyways, I will start anew tomorrow with new founded wisdom, I think I know how to do this now. Let me also try not to plug and chug and see if it helps me out

https://emojipedia.org/loudly-crying-face​

 

[Steve4Physics]

But yeah, the very algebra of it was tiring and frankly annoying to work through, do anyone of you have tips on that?

@kuruman's approach in Post #7 has much simpler algebra. You might like to consider the height-time graph for object1:

Edit - cosmetic changes.

 

[kuruman]

So after substituting values from the equation I am wrong or was this a tip to make the algebra easier than to just substitute immediately?

Absolutely, especially if you follow the method in post #7. I started posting the algebra here, but then I decided not to and let you do it to see for yourself.

 

[PeroK]

Absolutely, especially if you follow the method in post #7. I started posting the algebra here, but then I decided not to and let you do it to see for yourself.

It's only a few lines that way. No square roots; no quadratics!

 

[kuruman]

It's only a few lines that way. No square roots; no quadratics!

And no premature gesticulation, i.e. hand-waving right at the start.

 

[D H]

So after substituting values from the equation I am wrong or was this a tip to make the algebra easier than to just substitute immediately?

That was a strong hint. Newcomers tend to substitute values (e.g., $H=4.0\m\text{m}$) as soon as they can. Refrain from doing that. Plugging in values at the very last second rather than very first second tends to give more insight.

 

[Orodruin]

Always use symbolical values for as long as you can get away with it. Not only does it make the functional dependence much clearer, it also allows for easier dimensional analysis and testing your result in different limits.

That said, I may be weird, but I solved it by drawing two straight lines in a graph ...
(I too get a rational quotient)

 

[PeroK]

I can't lie I fail to see how this helps me

Are you still stuck? I've checked and it's definitely not $2.4m$.

 

[stabby_faris]

Are you still stuck? I've checked and it's definitely not $2.4m$.

yuh I thought so it wasn't. I am struggling to see you guys' point of view. I have very weak visual imagery

 

[stabby_faris]

Take a step back from the problem and think what you have here. Because of the initial horizontal velocities, this is really a 1D free fall problem. Imagine looking at the shadows of the two objects projected on a vertical wall.
Shadow 2 drops down from A to B in time $t_2.$
Shadow 1 drops down from A to the floor and then back up to B in time $t_1.$
Let $T_{\text{AA}}$ be the time it takes for shadow 1 to make the round trip from A back to A. Because $T_{\text{AB}}=T_{\text{BA}}$, it follows that
$t_2=T_{\text{AA}}-t_1$. That's one relation between $t_1$ and $t_2$. You need to look at what's happening in the horizontal direction to find a second relation and then put the two together to find $h$. What do you think that relation looks like?

So they reach the same h height point where the bouncing ball reaches it twice, once before and once after.

And, considering their horizontal velocities, one ball reaches it in half the time as opposed to the bouncing one *after* it bounces. But how can I relate this to height?

 

[PeroK]

yuh I thought so it wasn't. I am struggling to see you guys' point of view. I have very weak visual imagery

One final simplifying idea is to let $d = H - h$. And calculate $d$.

The basic idea is that the second projectile falls a distance $d$ before hitting the bulb. This happens in time $t_2$. And the first projectile falls a distance $H$, then bounces back up a distance $h = H - d$. And, this all happens in a time $t_1 = 2t_2$.

Finally, $t_1 = 2T - t_2$. This comes from the time symmetry of the SUVAT equations. You can crank this out algebraically easily enough, if you don't see it. That would be a separate exercise for an elastically bouncing ball.

PS Where $T$ is the time to fall to the ground; or, equally, to bounce back up to height $H$. The equality, again, comes from symmetry of the equations. Or, can be shown algebraically.

 

[stabby_faris]

One final simplifying idea is to let $d = H - h$. And calculate $d$.

The basic idea is that the second projectile falls a distance $d$ before hitting the bulb. This happens in time $t_2$. And the first projectile falls a distance $H$, then bounces back up a distance $h = H - d$. And, this all happens in a time $t_1 = 2t_2$.

Finally, $t_1 = 2T - t_2$. This comes from the time symmetry of the SUVAT equations. You can crank this out algebraically easily enough, if you don't see it. That would be a separate exercise for an elastically bouncing ball.

PS Where $T$ is the time to fall to the ground; or, equally, to bounce back up to height $H$. The equality, again, comes from symmetry of the equations. Or, can be shown algebraically.

But that approach literally requires quadratics and was the algebraic headache I was talking about

 

[kuruman]

And, considering their horizontal velocities, one ball reaches it in half the time as opposed to the bouncing one *after* it bounces. But how can I relate this to height?

To summarize, you already got two equations using the notation in post #22
$t_1=2t_2$
$t_1=2T-t_2.$
Here $T$ is the time it takes object 1 to hit the floor and you an easily find it in terms of $H$ and $g$.
Add to the above an equation that says that in time $t_2$ object 2 drops to a distance $H-h$.

You now have a system of three equations and three unknowns, $t_1$, $t_2$ and $h$. Solve it.

 

[PeroK]

But that approach literally requires quadratics and was the algebraic headache I was talking about

The algebra required is pretty simple.

 

[kuruman]

But that approach literally requires quadratics and was the algebraic headache I was talking about

You are foreseeing headaches where there are none. Nothing more involved than $\left(\sqrt{a}\right)^2=a.$

 

[stabby_faris]

nah bruh I am stuck

To summarize, you already got two equations using the notation in post #22
$t_1=2t_2$
$t_1=2T-t_2.$
Here $T$ is the time it takes object 1 to hit the floor and you an easily find it in terms of $H$ and $g$.
Add to the above an equation that says that in time $t_2$ object 2 drops to a distance $H-h$.

You now have a system of three equations and three unknowns, $t_1$, $t_2$ and $h$. Solve it.

I literally can't even get a train of thought anymore

 

[kuruman]

nah bruh I am stuck

I literally can't even get a train of thought anymore

Then perhaps you need to take a break and come back to this later, bruh. The task is this

An object is released from rest at height $H$ above ground. It takes time $t_2$ to drop to new height $h$ above ground. Write the appropriate kinematic equation that expresses this.

 

[stabby_faris]

Then perhaps you need to take a break and come back to this later, bruh. The task is this

An object is released from rest at height $H$ above ground. It takes time $t_2$ to drop to new height $h$ above ground. Write the appropriate kinematic equation that expresses this.

Wait I am goated, h = 2.22 metres?

I was analyzing my approach versus you guys and I finally realized where I made it hard for myself, I did not exploit symmetry, which I know IPhO problems love

Then I realized that with system of 3 equations I get overwhelmed pretty damn easily and made it hard for myself on which ones I substitute smh.

Thank you for your patience guys, I will shout you out incase I am interviewed in IPhO so stay tuned, look for a dude named Faris (its looks hopeless but I will reach there dw)

Love yall!

 

[kuruman]

Then I realized that with system of 3 equations I get overwhelmed pretty damn easily and made it hard for myself on which ones I substitute smh.

It looks like you allowed the number 3 to intimidate you without really looking at the equations with an eye towards figuring out your approach. From
$t_1=2t_2$
$t_1=2T-t_2.$
it follows that $2t_2=2T-t_2 \implies t_2=\frac{2}{3}T.$
Can you finish it now?