Find the Lagrangian of a pendulum plane

[LCSphysicist]

Homework Statement

Pendulum plane, which suspension executes a harmonic motion.

Relevant Equations

\n

Pendulum plane, which suspension executes a horizontal harmonic motion $$x = acos(\gamma t)$$

Position P, orientation x to right and y points below, phi is the pendulum's angle wrt y.

$$P = (acos(\gamma t) + lsin(\phi(t)), lcos(\phi(t)) )$$

So executing all that is necessary, i found it, after eliminates explicit dependence (and only dependence) of time

$$\frac{m(l^2\dot{\phi }^{2} -2la\gamma \dot{\phi }cos(\phi )sin(\gamma t)) }{2} + mglcos(\phi )$$

BUt the answer is:

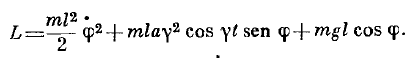
Not sure about this middle term, is it right?

 

[BvU]

A dimension check can disprove one of the two ...

 

[LCSphysicist]

A dimension check can disprove one of the two ...

I don't see it.
$mla \gamma^2$ has the same unit as $mla \gamma \dot{\phi}$
$\gamma$ and $\dot{\phi}$ has unit $s^{-1}$

 

[BvU]

Ah, sorrry, you are correct. My bad. So we have to check the

executing all that is necessary, i found

Can you please post it ?

And what is

after eliminates explicit dependence (and only dependence) of time

 

[LCSphysicist]

$$P = (acos(\gamma t) + lsin(\phi(t)), lcos(\phi(t)) )$$
$$v = (-asin(\gamma t)\gamma + lcos(\phi(t))\dot{\phi}, -lsin(\phi(t))\dot{\phi} )$$
$$U = -mg(lcos(\phi(t)) $$
$$L = m(-asin(\gamma t)\gamma + lcos(\phi)\dot{\phi})^2 + (lsin(\phi)\dot{\phi})^2))/2 + mg(lcos(\phi)$$
$L = m((asin( \gamma t) \gamma)^2 + (l \dot{\phi})^2 - 2asin(\gamma t) \gamma lcos(\phi) \dot{\phi})/2 + mgl(cos(\phi))$

Taking $m((asin( \gamma t) \gamma)^2$ off we get my answer.

I know it is strange, but Landau did it too, as he said in the solution, he takes off this terms. I don't know why, but it makes sense so i follow it.
Makes sense because when we will need to calc the $$\frac{\partial L}{\partial q}-\frac{d}{dt} \frac{\partial L}{\partial \dot q}=0$$ we wil not need this terms at all

 

[TSny]

Two Lagrangians yield the same equations of motion if they differ by a total time derivative of some function of the coordinates and time. See the 4th paragraph of page 4 in Landau. Show that your middle term differs from Landau's middle term by a total time derivative.