- #1
JulienB
- 408
- 12
Homework Statement
Hi everybody! I'm back with another lagrangian problem :) Although I think (or hope) I have made progress on the topic, I always learn a lot by posting here!
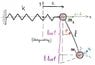
A pendulum with point-shaped mass ##m_1## hangs on a massless string of length ##l##. The suspension point (also a mass point) of the pendulum has mass ##m_2## and can move horizontally without friction. The force ##\vec{F} = -kx\vec{e}_x## applies on the suspension point, while the gravity force applies on the pendulum mass point. The motion of the pendulum takes place in the plane of projection.
a) Determine the Lagrange function for suitable generalized coordinates.
b) Derive the equations of motion.
Homework Equations
Lagrange function (##L = T - V##)
The Attempt at a Solution
a)
Okay so I've attached a picture to show how I understand the situation. I called ##v_1 = \dot{x}## the velocity applying on ##m_2## because of the spring force and ##v_2## the velocity applying on ##m_1## because of the gravity. ##v_1## and ##v_{2_x} = l \dot{\varphi} \cos \varphi## apply in the x-direction, while ##v_{2_y} = -l \dot{\varphi} \sin \varphi## is the only velocity applying in the y-direction. From there I try to determine the kinetic energy of the system:
##\frac{1}{2} m_1 [(v_{2_x} + \dot{x})^2 + v_{2_y}^2] + \frac{1}{2} m_2 \dot{x}^2##
Here is one of the few points where I feel unsure: is it correct to consider so to say "twice" the velocity ##\dot{x}## (by that I mean that it is associated to ##m_1## and to ##m_2##)? I think yes because the motion is happening both for ##m_1## and ##m_2## and there's no reason that the motion of one or the other would not mean kinetic energy, but I'd love a confirmation :)
I went further anyway assuming that it was correct and after a few simplifications I got:
##T = \frac{1}{2} m_1 ( l^2 \dot{\varphi}^2 + 2 l \dot{\varphi} \cos \varphi \dot{x} + \dot{x}^2) + \frac{1}{2} m_2 \dot{x}^2##
Then for the potential energy I took the origin as shown on my drawing, this making ##kx## positive so to say:
##V = \frac{1}{2} k x^2 - m_1 g l \cos \varphi##
And therefore that would be my answer to question a:
##L = \frac{1}{2} m_1 ( l^2 \dot{\varphi}^2 + 2 l \dot{\varphi} \cos \varphi \dot{x} + \dot{x}^2) + \frac{1}{2} m_2 \dot{x}^2 - \frac{1}{2} k x^2 + m_1 g l \cos \varphi##
b)
So here is my second big doubt in that process: when it is asked to determine the "equationS of motion", does that basically mean ##\frac{d}{dt} \frac{\partial L}{\partial \dot{\varphi}} - \frac{\partial L}{\partial \varphi} = 0## and ##\frac{d}{dt}\frac{\partial L}{\partial \dot{x}} - \frac{\partial L}{\partial x} = 0##? And if so, do I have to mix them up or is it just convenient to have them so that you can solve for ##\varphi## or ##x## depending on your needs?
Anyway if that's right I've done the derivations and got:
##\ddot{\varphi} + \frac{\cos \varphi}{l} \ddot{x} + \frac{\sin \varphi}{l} g = 0##
##\ddot{x} + \frac{m_1}{m_1 + m_2} l(\ddot{\varphi} \cos \varphi - \dot{\varphi}^2 \sin \varphi) = 0##
I find it interesting that the first equation has no mass in it... Did I do something wrong or is there something to understand behind that? Even if I've seen that in other instances, the ##g## feels strange without the mass.Thanks a lot in advance for your answers, I appreciate it!Julien.