Find the Net Torque on Pulley with Masses M1 and M2

[Gravitino]

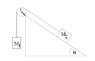
Two blocks of masses $$M_1$$ and $$M_2$$ passes through a pulley (See the Fig. attached.). Assuming the friction between block and the incline is zero, and neglecting the mass of string find the net torque about the center of mass of the pulley.

I solved this problem with two different ways. The answers are different. Please, let me know, where I am wrong.

1) $$\tau=\left(M_1-M_2\sin\theta\right)gR$$ because the net torque is due to external forces.

2) On the other hand, $$\tau=\left(T_1-T_2\right)R$$. And the tensions $$T_1$$ and $$T_2$$ are found from

$$M_1g-T_1=M_1a$$
$$-M_2\sin\theta g+T_2=-M_2a$$

The solution gives different answer. In the case, $$a=0$$, the two solution matches.

Which one is correct?

 

[Dick]

The second one is correct. So far you only have two equations in three unknowns, but there is also a third equation involving the rotational motion of the pulley, which also involves the torque (hence T1 and T2) and relates it to the angular acceleration of the pulley (which is related to a).

 

[Doc Al]

1) $$\tau=\left(M_1-M_2\sin\theta\right)gR$$ because the net torque is due to external forces.

Net torque on what?

2) On the other hand, $$\tau=\left(T_1-T_2\right)R$$. And the tensions $$T_1$$ and $$T_2$$ are found from

That's the net torque on the pulley. You need to apply Newton's 2nd law here as well.

$$M_1g-T_1=M_1a$$
$$-M_2\sin\theta g+T_2=-M_2a$$

Looks like you have a sign problem between these equations.

The solution gives different answer. In the case, $$a=0$$, the two solution matches.

Which one is correct?

What was your solution using method 1? You found the net torque, but didn't continue. (Hint: Too hard!)

Method 2 will give you the answer (if you correct the signs) and continue. That's the way to go.

(Dick's way ahead of me!)

 

[Gravitino]

The second one is correct. So far you only have two equations in three unknowns, but there is also a third equation involving the rotational motion of the pulley, which also involves the torque (hence T1 and T2) and relates it to the angular acceleration of the pulley (which is related to a).

Thanks. But i have still doubt. The first solution states that the net torque about the center of pulley, is just due to the external forces. They are the one which rotate the pulley. And Obviously, $$\tau=F_{net}R$$. And external forces are just gravity.

 

[Gravitino]

Net torque on what?

What was your solution using method 1? You found the net torque, but didn't continue. (Hint: Too hard!)

Method 2 will give you the answer (if you correct the signs) and continue. That's the way to go.

(Dick's way ahead of me!)

Net torque about center of pulley, you are right. For the first method, as i explained above, $$\tau=F_{net}R$$ and $$F_{net}=M_1g-M_2g\sin\theta$$.

In the second one,

$$M_1\sin\theta g-T_1=M_1a$$
$$-M_2\sin\theta g+T_2=M_2a$$

and the answers stiull do not match.

 

[Dick]

The 'external forces' aren't the gravitational forces, they are the tensions in the string. The tensions in the strings will depend on such things as the moment of inertia of the pulley. Pretend there is only the hanging mass. If the mass is heavy and the pulley is light, the downward acceleration will be almost g and the tension in the string will be much less than mg. If the mass is light and the pulley is heavy, then acceleration down will be much less than g and the tension in the string will be almost mg.

 

[Doc Al]

Thanks. But i have still doubt. The first solution states that the net torque about the center of pulley, is just due to the external forces.

The net torque on the entire system--pulley and the two masses--is just due to external forces acting on the system.

They are the one which rotate the pulley.

No. The tension forces act on the pulley to rotate it, not the weight of the masses. If you analyze the pulley, the tension forces are external to it. But if you analyze the entire system as a whole (not recommended), then you can say that the external forces are the weights of the masses.

The problem with method 1: You think you're finding the torque on the pulley, but you're not; you're finding the torque on the entire system. (That's why I asked: Torque on what?)

 

[Gravitino]

The 'external forces' aren't the gravitational forces, they are the tensions in the string. The tensions in the strings will depend on such things as the moment of inertia of the pulley. Pretend there is only the hanging mass. If the mass is heavy and the pulley is light, the downward acceleration will be almost g and the tension in the string will be much less than mg. If the mass is light and the pulley is heavy, then acceleration down will be much less than g and the tension in the string will be almost mg.

Thanks! I got it!

 

[Gravitino]

The net torque on the entire system--pulley and the two masses--is just due to external forces acting on the system.

No. The tension forces act on the pulley to rotate it, not the weight of the masses. If you analyze the pulley, the tension forces are external to it. But if you analyze the entire system as a whole (not recommended), then you can say that the external forces are the weights of the masses.

The problem with method 1: You think you're finding the torque on the pulley, but you're not; you're finding the torque on the entire system. (That's why I asked: Torque on what?)

Thanks!