chucho11028
- 9
- 0
- Homework Statement
- find rate of change of velocity
- Relevant Equations
- Vy=vi*sin(angle)
Vx=vi*cos(angle)
Ymax=vi*t-(g*t^2)/2
Xmax=vi*t
Hello everyone,
I have a problem where I have to find the final displacement and final velocity which I have found however, I want to post few variations for that same problem which I am curious. It is more for my own knowledge > I would appreciate any help
Please follow graph below with data:
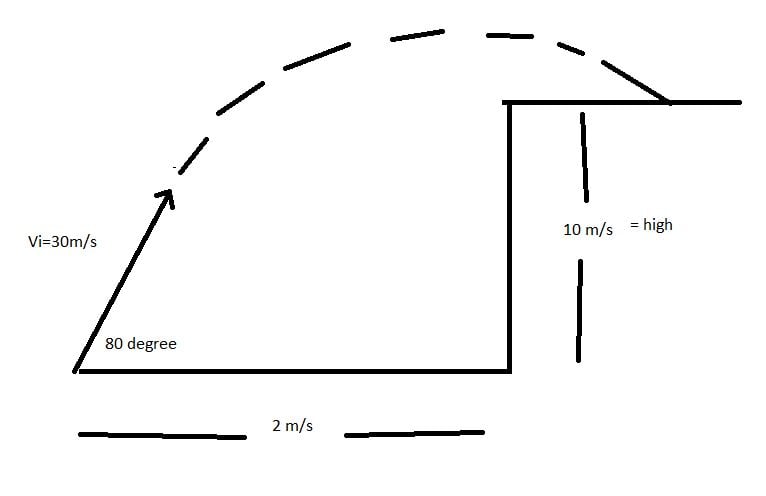
A projectile has been launched with Initial velocity 30 m/s, 80 degree elevation, there is 2 m in the x coordinate and 10 m high
In order to find final velocity I got delta t (second grade equation)
so, t= 5.67 seconds
then, total displacement is
which is equal to 29.53
then, I used Phythagoras and I got the relationship between 29.53 and 10 m high to find the displacement
which is 31.18 m
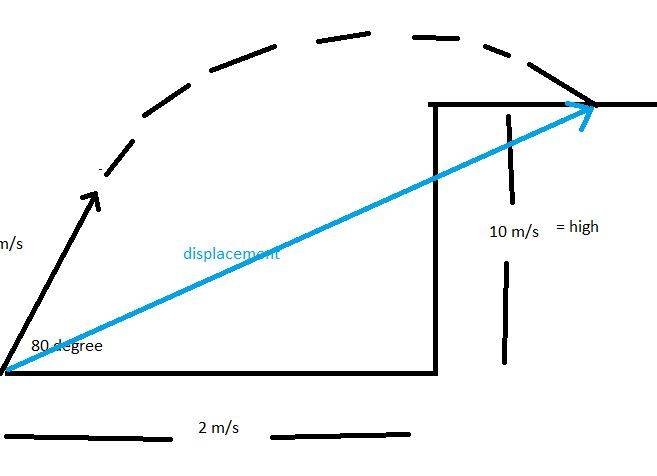
you can see the blue line
Then I can find the Vf using this idea
variation of V is equal vf-vi which is equal to g* t
then, my VF will be -26.03 m/s
Here is my question or some questions,
1. I assume is negative because the object is falling down, isn't it?
2. Then, the Vi (initial velocity) is positive because is in opposed direction, isn't it?
3. So, I think the velocity will be zero in the vertex of the parabola, isn't it
4. I think is I derive the equation for displacement , I will get the equation for velocity but what is the exact equation for displacement that represent this exercise ?
5. How can I find the vertex using the derive? Can I take displacement, then put equal to 0 and find the solution? I would need a help for this question
I have a problem where I have to find the final displacement and final velocity which I have found however, I want to post few variations for that same problem which I am curious. It is more for my own knowledge > I would appreciate any help
Please follow graph below with data:
A projectile has been launched with Initial velocity 30 m/s, 80 degree elevation, there is 2 m in the x coordinate and 10 m high
In order to find final velocity I got delta t (second grade equation)
Code:
10=29.54*t-4.9*t^2so, t= 5.67 seconds
then, total displacement is
Code:
Sx=30*cos80 * 5.67which is equal to 29.53
then, I used Phythagoras and I got the relationship between 29.53 and 10 m high to find the displacement
which is 31.18 m
you can see the blue line
Then I can find the Vf using this idea
variation of V is equal vf-vi which is equal to g* t
then, my VF will be -26.03 m/s
Here is my question or some questions,
1. I assume is negative because the object is falling down, isn't it?
2. Then, the Vi (initial velocity) is positive because is in opposed direction, isn't it?
3. So, I think the velocity will be zero in the vertex of the parabola, isn't it
4. I think is I derive the equation for displacement , I will get the equation for velocity but what is the exact equation for displacement that represent this exercise ?
5. How can I find the vertex using the derive? Can I take displacement, then put equal to 0 and find the solution? I would need a help for this question