Find the resistance through a resistor

[Resmo112]

Homework Statement

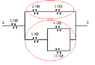
For the following questions, use the schematic below, where R1 = 3.0 Ω and R2 = 17.0 Ω.

(a) What is the equivalent resistance between points A and B for this combination of resistors?
3.83 Ω

(b) A 8-V emf is connected to the terminals A and B. What is the current through the 1.0-Ω resistor connected directly to point A?
2.1 A
(c) What is the current in the resistor R2?

Homework Equations

P=I^2*R
V=R*I

The Attempt at a Solution

now I got part A and part B was just the voltage on B divided by A. But I can't figure out how part C is different. Because i used the ohms for all of the resistors added together and I'm confused as to how that's different? I've included a screenshot.


http://imageshack.us/photo/my-images/196/screenshot20110609at608.png/"

 

[wbandersonjr]

Remember, how are the currents related, through two resistors that are connected in series? parallel? The current through R2 will not be equal to the current through the 1.0$\Omega$ resistor.

 

[Resmo112]

ok so if they're in parallel it's 1/R+1/R while if they're in series they're just R+R so should I do the same calculation and just put it to the -1?

 

[wbandersonjr]

That is how you add resistors. How about the current, is the current through two resistors that are in series the same? different? what is difference? what about two resistors that are in parallel? same? different currents? what is difference?

 

[wbandersonjr]

You need to use V=IR and work backwards after you find the overall equivalent resistance. Just like you step by step added the resistors that are in series and parallel, you need to separate them and figure out the needed information about V and I. For certain combinations the current through both is equal, through certain arrangements the voltage is equal, others they are not equal. You need to use all that info to work back to R2

 

[Resmo112]

the current is split between the two resistors I thought but I guess the current would be reduced to the point when the current is split between two resistors? I think I'm a little more confused.

 

[Resmo112]

ok so I need to figure out what the current is at the point before that resistor splits, and then divide that current by two because the current would be the same in each, so if I had 8V and it was passing through a 1ohm resistor it would have 8 amps going through it, then the next is 2 so it has 4 amps going through it, then a 3ohm resistor so 1.33 and then a 17 ohm resistor so .04? that can't be right.

 

[wbandersonjr]

Your right, the current is split between two resistors, when they are connected in parallel. In series, the current has no choice but to move through both resistors one after the other, the current is the same for both, and equal to the current through the equivalent resistor. Ok?

Now voltage is similar, but reversed. Two resistors in parallel, have each one side connected to the high potential side and one side connected to the low potential side, so the voltage is the same across the resistors, and equal to the voltage across the equivalent resistor. With resistors in series, the voltage drops across the first resistors and then drops again across the second. The voltage across the equivalent resistor is split between the two. Ok?

The key is that the relationship is opposite for the two cases so using V=IR, you can find the unknown that is different for each resistor, because the other quantity will be the same for both, equal the the value for the equivalent resistor. Ok?

 

[wbandersonjr]

What you need to do is say the final equivalent resistance is 3.83$\Omega$ (just using your number, i didnt verify if it's correct). Then the voltage is 8V (given) and then calculate the current through it so I=8/3.83. Next look at the next situation backwards, so you have a 1$\Omega$ resistor and the equivalent of all the others, and they are in series. So series, the current is the same through both, 8/3.83. Then, calculate the voltage through each, V=IR, so for the 1$\Omega$, V=1*(8/3.83). For the other resistor, V=R(equivalent) * (8/3.83). Then just continue this way until you get to R2.

 

[Resmo112]

no and I feel like an idiot here. If I'm working my way through resistors I can just add them all if I'm not mistaken because they're in series (until I get to the parallel ones) so if I have a 1 a 2 and a 3 ohm resistor then I should have 8/3.83 (which is right that part of the problem I know I did right) which is roughly 2.1 so multiply that by 6 but that increases the voltage which shouldn't it decrease it? it's a resistor? the sad thing is I have the frisking solution to this and I still can't get it.

 

[wbandersonjr]

If you had a 1, 2, and 3 $\Omega$ resistors in series, the equivalent would be 6$\Omega$, yes. Then the current through the equivalent would be I=8/6. The 8/3.83 is for your homework problem, which is totally different to the 1,2,3 combination.

Your homework ends with one 3.83$\Omega$ equivalent resistor. That was a combination of a 1$\Omega$ and 2.83$\Omega$ resistor, which were in series correct? R2, the resistor in question is one part of that 2.83$\Omega$ resistor so focus on that one... That was a combo of two parallel resistors... the bottom was a combo of two in series... and the one on the right was a combo of R2 and the 4$\Omega$ resistor.

But, the series and parallel combos, as you work back towards the R2 need either a value for current or voltage. The key is that when you break an equivalent resistor into two in series, the current through both is equal to the current through the equivalent one.

In the question you need the current through R2, to find that using V=IR, you need to know the voltage. The voltage will be the same as the voltage across the equivalent resistor of R2 and the 4$\Omega$ resistor. But you don't know that and need to find that... So what you do is work backwards from the one single equivalent resistor and find the current and voltage values as you work backwards breaking up equivalents on the way back to R2

 

[wbandersonjr]

Don't feel like an idiot. It is tricky, confusing, and time consuming. I hope I am explaining this well...

 

[Resmo112]

I'm down to three fricking attempts and I'm pretty sure I've wasted everyone. the 3.83 resistor was a combination of all the resistors in a series, so a 1 2 3 and a 1/17 1/4 and 1 3.3 resistor. what I don't understand is the working backwards? should I just work forward and add the resistors the divide that by the voltage?

 

[gneill]

Hi Resmo112. May I jump in here?

You've found the equivalent resistance of the whole network, and through that have found the current flowing from A to B (or B to A, depending upon the polarity of the battery connection!). If you now consider how a current divider works, I think you'll be on your way to solving the problem.

If you have a current that's presented with two possible paths to follow before joining up again "downstream", then the current divides between the paths in the following manner.

Suppose path 1 presents a resistance R1 and the other, path 2, the resistance R2. Then the current divides with the greater current flowing through the path with the least resistance. Mathematically it turns out that:

$$I1 = I \frac{R2}{R1 + R2}$$
$$I2 = I \frac{R1}{R1 + R2}$$

In your circuit you have a couple of situations where this occurs. First you have the current entering node A, passing through the 1.0 Ω resistor, and then splitting between the upper path and lower paths (One with your resistor R1 in it, and the other with resistor R2 buried in another path split). So, if you happen to know the total resistances of those individual paths (see attached diagram) then you can determine the amount of current that will flow into each branch.

If you then have the current flowing into the lower branch, it passes first through the 3.3 Ω resistor and then splits between the 4.0 Ω resistor and your R2, the 17 Ω resistor. You can perform the same "trick" with these paths to find the current through the 17 Ω resistor.

Let me know if this is too cryptic to decipher and I'll try to clarify further.

 

[Resmo112]

it's a little cryptic. very detailed but I think if you put it in caveman speak it might help. I'm trying to figure out how I can solve one of those two equations for the current but I don't think I can. physics 2 is such a migraine it's silly. not to mention I've got a whole nother problem that I should have the answer too but can't get it.

 

[gneill]

Okay. Consider the circuit fragment in the attached figure. A current I enters from the left and at the node marked a splits into two separate paths with different resistances R1 and R2, then rejoins at he node marked b before continuing on. The current that "chooses" to flow through resistance R1 is I₁, and the current through R2 is I₂.

Clearly I₁ + I₂ = I. The current divides so that

$$I_1 = I \frac{R2}{R1 + R2}$$
$$I_2 = I \frac{R1}{R1 + R2}$$

Note that if you add I₁ and I₂ you get

$$I_1 + I_2 = I \frac{R1 + R2}{R1 + R2} = I$$

Alright so far?

Example: Suppose I is 10 Amps, R1 is 3Ω and R2 is 7Ω. Then the current through R1, the 3Ω resistor, is

10A * 7Ω/(3Ω + 7Ω) = 10A * 7/10 = 7 Amps.

Now in your circuit the first such split occurs after the current passes through the 1Ω resistor. In my previous post I circled the components in the two paths.

If you can find the total resistances of these individual paths, then you can apply the current divider rule to find the current flowing into the lower path. Next, armed with the current entering this path, you can face the split contained within it in a similar fashion; the current in the lower path divides between the 4.0Ω resistor and your 17Ω resistor. Your aim is to find the current that flows in that 17Ω resistor.

 

[Resmo112]

ok I actually think I see where I was going wrong. A) i didn't exactly realize there were two paths I thought it was a closed circuit. B) I blow at this. that aside.

so my circuit with 8v attached went from a to b so my voltage was 8v so 8v = I 3.3/17+4 solve for I except that really isn't the voltage, this is where I'm running into a hiccup. it has to split after the it goes through that 1 ohm resistor. or do I use the 2.1 = I 3.3/17+4? am i getting close?

 

[Resmo112]

no neither of those can be right? would it just be 2.1*3.3/17+4?

 

[Resmo112]

ok that doesn't work either? wait I'm missing something? because your equations only have 2 resistors and I need to include 3 resistors? but if I'm adding resistance shouldn't it be 3.3 + (1/17+1/4)^-1?

 

[gneill]

The explanation that I gave for the current divider was just to show the principle, so it only included the necessary minimum of components.

I notices that previously you determined the total current supplied by the battery. That was, what, 2.087A? (I keep a few extra decimal places for intermediate results -- avoids rounding errors making a hash of things later). That current will be entering the network at node A, and leaving by node B.

What's the numerical values of the resistances for the two paths that I had previously indicated by red circles?

 

[Resmo112]

yeah I rounded up to 2.1 but 2.089 I think was may actual value. the second path the one we're working on has a 3.3 ohm resistor then two broken into parallel resistors of 4 and 17ohms. for the first path it's just a series of a 2 and 3 ohm resistor.

 

[gneill]

yeah I rounded up to 2.1 but 2.089 I think was may actual value. the second path the one we're working on has a 3.3 ohm resistor then two broken into parallel resistors of 4 and 17ohms. for the first path it's just a series of a 2 and 3 ohm resistor.

Yes, and their net resistances are...?

 

[Resmo112]

sorry for the first path it's 5 because you just add the resistances, and for the second it's 6.54 if I'm figuring it out right.

3.3 +(1/17+1/4)^-1

 

[Resmo112]

please don't tell me the answer to this question is 8v/6.54?

 

[Resmo112]

and that I just had to sum up the resistance and then do EXACTLY what I did on the previous problem and for some reason it's been the most difficult thing in the world for me?

 

[gneill]

sorry for the first path it's 5 because you just add the resistances, and for the second it's 6.54 if I'm figuring it out right.

3.3 +(1/17+1/4)^-1

Correct. So now with the total current and these two resistances you can find the current that's entering the lower path using the current divider method. Can you do that and show the result?

 

[Resmo112]

OHHH so my total current is the 8 volts and my R1 = 5 and my R2 = 6.54 so if I wanted to find I2 I'd do I2= 8 *(6.54/5+6.54)

 

[Resmo112]

no that's just finding the current going through the bottom half of my bigger part of the resistor and I have to find the current through R2 so I would have to take that current and then do the same process over?

 

[gneill]

OHHH so my total current is the 8 volts and my R1 = 5 and my R2 = 6.54 so if I wanted to find I2 I'd do I2= 8 *(6.54/5+6.54)

Sorry, no. 8V is a voltage, not a current. You calculated the total current driven by the 8V source previously. I = 2.087A. You did this by first finding the overall equivalent resistance of the network of resistors (call it R) and then calculating 8V/R. Right?

The current divider method works with currents, not voltages.

So, once again, can you calculate the current in the lower path?

 

[Resmo112]

that's where I'm starting to get confused. so if my current through the top half from a to B is 2.089(yes 8V/R is how I arrived at that.) but that's the current through 2 resistors, so I can't use that as my I value?

 

[gneill]

that's where I'm starting to get confused. so if my current through the top half from a to B is 2.089(yes 8V/R is how I arrived at that.) but that's the current through 2 resistors, so I can't use that as my I value?

2.087A is the total current flowing from A to B. After passing through the 1 Ohm resistor it splits into two paths, an upper path that has two resistors in series (2 and 3 ohms), and the bottom path containing three resistors in a slightly more complicated configuration. You want to find out how much of that original 2.087A is flowing via this bottom path.

You have calculated the total resistances of the two individual paths. You have the total current. You have the current divider rule. You want the current in the lower path. I don't know how I can be more explicit.

 

[Resmo112]

ok so I'm looking for my I2 if 2.087A is my I value then I need to put the resistor values into the R2/R2+R1 part of the equation.

I'm sorry dude I'm really trying I promise I am I really appreciate the patience, there's no reason this should be taking you this long.

is it just I2=2.087*(6.54/5+6.54)=1.18? the problem I have there is I don't understand why I'm using the top half of the circuit.

 

[gneill]

ok so I'm looking for my I2 if 2.087A is my I value then I need to put the resistor values into the R2/R2+R1 part of the equation.

I'm sorry dude I'm really trying I promise I am I really appreciate the patience, there's no reason this should be taking you this long.

is it just I2=2.087*(6.54/5+6.54)=1.18? the problem I have there is I don't understand why I'm using the top half of the circuit.

The current divider rule determines the fraction of the total current, I, that splits off and flows through a given path. If you look closely at the rule, it states that the fraction of the current that flows through a given path is equal to the resistance of the *other* path divided by the sum of the resistances of both paths.

By placing the resistance of the lower path in the numerator of the ratio, you've actually calculated the current flowing through the upper path rather than current in the lower path. So replace the 6.54 quantity in the numerator with 5, the resistance of the upper path. this will give you the current in the lower path. What value do you calculate?

 

[Resmo112]

ok so I got .904.
I did 2.087 * 5/6.54+5 and that = .904

 

[Resmo112]

but that's not the right answer either.