Find the Volume of Mt. Vesuvius After 79AD in Terms of pi

[ruu]

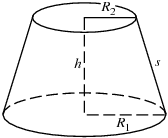
Mt. Vesuvius in Pompeii was a conic volcano with a height from its base 7950 feet and a base radius of 2300 feet. In 79 AD, the volcano erupted, reducing its height to 4200 feet . Find the volume of the volcano after 79 AD in terms of pi.


WORK:
Volume of Volcano(Before 79AD)= \pi *r^2*h/3
=\pi *(2300)^2 * 7950/3
=5290000\pi * 2650
= 1.4019 * 10^10 * \pi

Volume of Volcano part erupted off:
Height: 7950 ft - 2300 ft = 5650 ft
Radius= 5650 * (2300/7950) = 1634.5912 ft
Volume= \pi *r^2*h/3
= \pi *(1634.5912)^2*5650/3
=2671888.375 \pi * 1896.6667
=5067681707* \pi

Volume of Volcano(After 79AD)= (Volume of Volcano(Before 79AD)) - (Volume of Volcano part erupted off)
=(1.4019 * 10^10 * \pi) - (5067681707* \pi)
= 8951318293* \pi

Note to reader: Please check my work. I'm not sure if my solutions are correct or if i did the problem correctly.
Thank you!

 

[MarkFL]

We know the radius $r$ of the cone decreases linearly as a function of height $h$, and this linear function contains the two points:

$$(r,h)=(2300,0),\,(0,7950)$$

Thus, using the point-slope formula, we obtain:

$$r(h)=-\frac{2300}{7950}h+2300=2300\left(1-\frac{h}{7950}\right)=\frac{2300}{7950}(7950-h)$$

Now, the volume $V$ of the frustum of a cone is given as:

$$V=\frac{h}{3}\left(A_1+A_2+\sqrt{A_1A_2}\right)$$

where $$A_i=\pi R_i^2$$

Hence:

$$V=\frac{\pi h}{3}\left(R_1^2+R_2^2+R_1R_2\right)$$

With $h=4200\text{ ft}$, we obtain:

$$R_1=2300\text{ ft}$$

$$R_2=\frac{2300}{7950}(7950-4200)\text{ ft}=\frac{57500}{53}\,\text{ft}$$

And so, we have:

$$V=\frac{\left(4200\text{ ft}\right)\pi}{3}\left(\left(2300\text{ ft}\right)^2+\left(\frac{57500}{53}\,\text{ft}\right)^2+\left(2300\text{ ft}\right)\left(\frac{57500}{53}\,\text{ft}\right)\right)$$

$$V=\frac{35245154000000}{2809}\pi\text{ ft}^3\approx1.2547224635101458\times10^{10}\text{ ft}^3$$

This is different than your result. I see the reason is that when you computed the volume of the part blown off, you computed the height of the part blown off by taking the initial height and subtracting the base radius, when you should have subtracted the final height instead. :)

 

[ruu]

We know the radius $r$ of the cone decreases linearly as a function of height $h$, and this linear function contains the two points:

$$(r,h)=(2300,0),\,(0,7950)$$

Thus, using the point-slope formula, we obtain:

$$r(h)=-\frac{2300}{7950}h+2300=2300\left(1-\frac{h}{7950}\right)=\frac{2300}{7950}(7950-h)$$

Now, the volume $V$ of the frustum of a cone is given as:

$$V=\frac{h}{3}\left(A_1+A_2+\sqrt{A_1A_2}\right)$$

where $$A_i=\pi R_i^2$$
Hence:

$$V=\frac{\pi h}{3}\left(R_1^2+R_2^2+R_1R_2\right)$$

With $h=4200\text{ ft}$, we obtain:

$$R_1=2300\text{ ft}$$

$$R_2=\frac{2300}{7950}(7950-4200)\text{ ft}=\frac{57500}{53}\,\text{ft}$$

And so, we have:

$$V=\frac{\left(4200\text{ ft}\right)\pi}{3}\left(\left(2300\text{ ft}\right)^2+\left(\frac{57500}{53}\,\text{ft}\right)^2+\left(2300\text{ ft}\right)\left(\frac{57500}{53}\,\text{ft}\right)\right)$$

$$V=\frac{35245154000000}{2809}\pi\text{ ft}^3\approx1.2547224635101458\times10^{10}\text{ ft}^3$$

This is different than your result. I see the reason is that when you computed the volume of the part blown off, you computed the height of the part blown off by taking the initial height and subtracting the base radius, when you should have subtracted the final height instead. :)

Hello, thank you for your help so far.However, how can I find the final volume of the volcano after 79 AD without the knowledge of the volume of a frostum.
For example, can you solve this problem by subtracting the total volume of the volcano before 79AD minus the volume of the part of the volcano that blew off? And how?

 

[MarkFL]

Hello, thank you for your help so far.However, how can I find the final volume of the volcano after 79 AD without the knowledge of the volume of a frostum.
For example, can you solve this problem by subtracting the total volume of the volcano before 79AD minus the volume of the part of the volcano that blew off? And how?

I used the formula for the volume of a conical frustum as a means of checking your work, as you requested. Once I found that gave a result different from what you posted, I looked through your work and found the error:

...This is different than your result. I see the reason is that when you computed the volume of the part blown off, you computed the height of the part blown off by taking the initial height and subtracting the base radius, when you should have subtracted the final height instead. :)

Make that correction and see if your result then agrees with the result I posted. :D