ermia
- 13
- 0
- Homework Statement
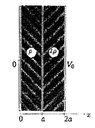
- Two infinite conducting plane are a distance 2a away and parrarel. We have constant potentials on the planes. In ##0<x<a## we have charge with density ##\rho## and in ##a<x<2a## with density ##2\rho##. We want to findelectric feild and potential everywhere. And to find the charge density in boundaries.
- Relevant Equations
- $$\nabla .E=\frac{ \rho}{\epsilon }$$
$$ E=- \nabla V$$
$$Eup -Edown = \sigma / \epsilon$$
I have wrote all feilds and potentials and I want to find the constants.
My first question is " when we say in the a<x<2a the potential is V(x)" then the potential in the a is V(a) or V(0) ( cause it is 0 in our new area) ?
Second one is " when I want to write the gausses law for the point x=a I find two feilds. Does that mean I have another surface charge in x=a?"
My first question is " when we say in the a<x<2a the potential is V(x)" then the potential in the a is V(a) or V(0) ( cause it is 0 in our new area) ?
Second one is " when I want to write the gausses law for the point x=a I find two feilds. Does that mean I have another surface charge in x=a?"