- #1
DannyPhysika
- 30
- 0
Homework Statement
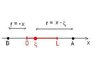
The plastic rod of the length L=1 m has a non-uniform charge density λ=cx where positive constant c =2x10^-6 [some unit]. What unit c has to have? Find the electric potential at the point on the x-axis 1 m to the left from the left end of the rod. Find the electric field at that point via potential. What is the direction of the field
Homework Equations
E = -dV/dx
The Attempt at a Solution
The first two parts I've solved. For the electric field:
I've gotten:-3.47 x 10^3 N/C
or
-1.45 x 10^4 N/C
But I'm not sure which is good. Thanks for any information :)