happyparticle
- 490
- 24
- Homework Statement
- find the magnetic field ##B## produce by ##C1## everywhere inside the coil.
- Relevant Equations
- ##C_1## where ##N=N_1## and ##I=I_1##
##C_2## where ##N=N_2## and ##I=I_2##
##\oint B \cdot dl = \mu_0 NI##
I have a toroid with square cross section and 2 different circuit:
##C_1## where ##N=N_1## and ##I=I_1##
##C_2## where ##N=N_2## and ##I=I_2##
I have a question that say I have to find the magnetic field ##B## produce by ##C_1## everywhere inside the coil. I assume here I have to find the magnetic field ##B## produce by ##C_1## everywhere inside the toroid.
I'm wondering if ##C_2## can affect the magnetic field caused by ##C_1## and I'm not sure how it works for a coil only around a little part on the toroid.
For exemple, If I have only a coil around the entire toroid, I can find the magnetic field using the Ampere's law.
##\oint B \cdot dl = \mu_0 NI##
##dl = 2\pi r##
##B = \frac{\mu_0 NI}{2\pi r}##
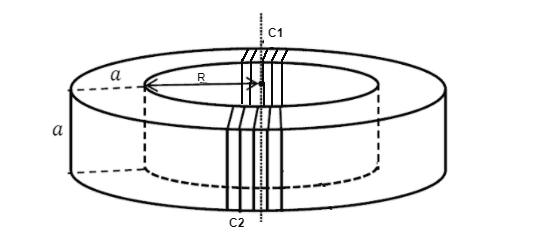
##C_1## where ##N=N_1## and ##I=I_1##
##C_2## where ##N=N_2## and ##I=I_2##
I have a question that say I have to find the magnetic field ##B## produce by ##C_1## everywhere inside the coil. I assume here I have to find the magnetic field ##B## produce by ##C_1## everywhere inside the toroid.
I'm wondering if ##C_2## can affect the magnetic field caused by ##C_1## and I'm not sure how it works for a coil only around a little part on the toroid.
For exemple, If I have only a coil around the entire toroid, I can find the magnetic field using the Ampere's law.
##\oint B \cdot dl = \mu_0 NI##
##dl = 2\pi r##
##B = \frac{\mu_0 NI}{2\pi r}##