Finding tension and acceleration in a 3 weight, 3 pulley system

[SovXietday]

Homework Statement

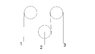
This is a "DOE" (Design of Experiment) problem. Basically, the construction is fairly simple. 3 pulleys, 2 on either side, and a free pulley with a weight suspended on it in the middle. Picture is available (don't mind my crappy paint skills, rope lengths are all parallel).

I basically need to compare theoretical velocity of C after falling 5cm and after falling 85cm to my actual measured velocities. However, to be honest my experimental values are all sorts of messed up, and I'm simply not sure if my math is anywhere near right.

m1 = .270kg
m2 = .522kg
m3 = .300kg

Homework Equations

F(net) = ma
xf = 1/2at^2 + volt + xi (dx/dt and dv/dt respectfully)

The Attempt at a Solution

First I set up my three equations.

m1g - T1 = m1a
T1 = m1g - m1a Eq1

2T2 - m2g = m2a
T2= 1/2(m2g + m2a) Eq2

m3g - T3 = m3a
T3 = m3g - m3a Eq3

So, Fnet = ma should be
T1 + T3 - T2 = ma (what is m? The mass sum of the system?)

Plug in.
m1g - m1a + m3g - m3a - 1/2m2g - 1/2m2a = ma
m1g + m3g - 1/2m2g = a(m + m1 + m3 + 1/2m2)

Isolate for a = (g[m1 + m3 - 1/2m2]) / (m + m1 + m3 + 1/2m2)

If I plug in what I *think* m is supposed to equal (1.092), I get a = 1.923m/s

Integrate a
Vf = 1.923t + Vo (Vo is 0)
Integrate vf
xf = .9615t^2 + xo (Xo is also 0)

Plug in .85m for Xf (furthest displacement of weight 3)
t = .94s

Vf = 1.923(.94)
Vf = 1.808 m/s at .85m

...not even close am I?

 

[ehild]

Do you know the mass of the pulleys? Or they should be assumed massless when calculating the theoretical velocities?

ehild

 

[SovXietday]

Masses of the pulleys are all 7grams. The mass of weight 2 already has the the entire pulley assembly + hanging weight added up. This is a real test, so everything applies.

Real problem is that the teacher has assigned this test for dynamics chapter 1 - rectilinear motion. That's fine if we have distances and velocities, but we don't "know" forces yet, so I'm trying to source all of these equations from backlogs of long ago physics homework and online teachings. :/

 

[ehild]

Which mass is C that falls 5 cm and 85 cm?

The problem is relatively easy if you can ignore the rotational inertia of the pulleys. It is rather complicated otherwise.

In the former case, the tension is the same in all pieces of the rope.
The acceleration of the masses are not the same, however. You need to find out how the acceleration of mass 1 and mass 3 are related to the acceleration of mass 2. Mass 2 is attached to two pieces of the rope. If mass 1 moves downward by Δy1 and mass 3 moves downward by Δy3, mass 2 must move upward by Δy2=(Δy1+Δy3). Take these into account in your equations. You get 3 equations with the unknown T and a1, a3.

ehild