Finding the distance of a peg so that a pendulum can circle around it

[SelzerRS]

Homework Statement

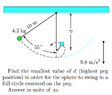
A pendulum made of a string and a sphere is able to swing in a vertical plane. The pendulum is released from a position of 55 ◦ from vertical. The string hits a peg located a distance d below the point of suspension and rotates about the peg. The acceleration of gravity is 9.8 m/s^2. Find the smallest value of d (highest peg position) in order for the sphere to swing in a full circle centered on the peg. Answer in units of m.

Relevant Equations

Ki+Ui=Kf+Uf
U=mgh
K=1/2(m*v^2)
Fc=(m*v^2)/r

Last time I posted to the forums I was told to use some type of text thing to make equations easier to read for clarity, but I can't figure it out, so sorry if this is hard to read.

I know that d = 10-r
After making a free-body diagram, I thought the circular force had to equal Tension + weight, so I set Fc = mg+T and solved for r
r =( m*v^2)/(mg+T)
I first used conservation of energy to find the velocity of the sphere:
I set when the sphere is the lowest at 0 m height and the suspension at 10 m height. B/c initial v=0, Ki=0 and b/c final height=0, Uf=0, so
Kf = Ui or (m*v^2)/2 = mgh so velocity must be v=sqrt(2gh)
I found the initial height of the sphere using the length of the pendulum and trig to find the height above it then subtract by 10.
h=10-(cos(55)*10)=4.264235 m
I plugged my numbers in and got
v=sqrt(2*9.8*4.264235)= 9.142156 m/s
Next I found Tension by drawing a free-body diagram and seeing it was in the opp direction of (mg)/cos(55).
I assumed that the two cancel each other so
(mg)/cos(55)=T
Plugged in the numbers and got
T = 71.7603 N
After finding T and v, I plugged my values back into the equation for r
r = (4.2*9.142156^2)/((4.2*9.8)+71.7603) = 3.10867 m
Then subtracted by 10 to get
d = 6.89133 m

Here's my scratchwork, I know it's messy but hopefully it better explains my thought process.

I think I might have gone wrong when finding tension, but it may also be my whole set up. Please let me know

 

[kuruman]

You are assuming that the tension at the moment of release at angle 55° when the speed is zero is the same as the tension when the mass is at the top of the trajectory. That is incorrect. The tension depends on both the speed and the angle.

Your equation $m\dfrac{v^2}{r}=mg +T$ was derived from the FBD at the top of the trajectory. Yet, you substitute 9.142156 (units?) for v which is the speed at the lowest point of the motion. That is plain wrong.

The problem is asking you to find the smallest of $d$ so that the mass describes a full circle. You need to think what that means. What would happen to the trajectory of the mass if the value of $d$ were smaller than that value? What would happen to the trajectory of the mass if the value of $d$ were larger than that value?

Also, please use symbols instead of numbers and substitute at the very end. Then you will not have to carry the variables to an absurd number of significant figures. It is very difficult to follow what you are doing from strings of numbers without units.

 

[SelzerRS]

Thank you! I realized I forgot to take into account the potential energy of the sphere at the highest trajectory. I'm working on learning how to use LaTex so that my work is easier to read next time