MHB Finding the Domain of a Logarithmic Function f(x) = log_5(8 - 2x)

[RidiculousName]

I need to find the domain of f(x) = log₅(8 - 2x).

I am not sure if I could find this by doing a inequality equation, but I think my professor wants us to do it on a number-line anyway. I'm sorry, but I am not sure where to start.

 

[MarkFL]

In order for a log function to return a real value, for:

$$f(u)=\log_a(u)$$

We require:

$$0<u$$

So, what inequality do we obtain from the given function?

 

[RidiculousName]

In order for a log function to return a real value, for:

$$f(u)=\log_a(u)$$

We require:

$$0<u$$

So, what inequality do we obtain from the given function?

8 - 2x > 0
-2x > 8
x > 8/-2
x > -4

so the domain is (-$$\infty$$, 4)
I'm trying to figure out how to do it via the number-line method though. I need to do it that way because otherwise I can't find the domain of stuff like, $$y = ln\frac{x - 1}{(x - 3)(x + 5)}[/math]

 

[MarkFL]

8 - 2x > 0

This is correct.

-2x > 8

This is not correct...if you are going to subtract 8 from both sides of the inequality, then you want:

$$-2x>-8$$

What I would have done is to add \(2x\) to both sides to get:

$$8>2x$$

Both approaches lead to:

$$x<4$$

In interval notation:

$$(-\infty,4)$$

This is what you eventually wound up with, but you got there from:

$$x>-4$$

and the end result does not follow from this.

I'm trying to figure out how to do it via the number-line method though. I need to do it that way because otherwise I can't find the domain of stuff like, $$y = ln\frac{x - 1}{(x - 3)(x + 5)}[/math]

To draw the solution on a number line, place an open circle at 4 (open circle because the inequality is strict), and shade to the left of that point.

View attachment 8431

 

[RidiculousName]

This is correct.
This is not correct...if you are going to subtract 8 from both sides of the inequality, then you want:

$$-2x>-8$$

What I would have done is to add \(2x\) to both sides to get:

$$8>2x$$

Both approaches lead to:

$$x<4$$

In interval notation:

$$(-\infty,4)$$

This is what you eventually wound up with, but you got there from:

$$x>-4$$

and the end result does not follow from this.
To draw the solution on a number line, place an open circle at 4 (open circle because the inequality is strict), and shade to the left of that point.

Whoops! Thank you, I had gotten the answer from my professor beforehand. There should be a way to figure out the problem without using an inequality though. That is what I am trying to understand how to use. I know it involves a number-line and, it seems like, you guess at possible values for x. For example, you couldn't find the domain of $$y = ln\frac{x - 1}{(x - 3)(x + 5)}$$ just by using inequalities right? I am trying to figure out how to find the domain of a logarithm like that. The approach should work regardless of whether you use this or the first logarithm I posted. I am not just trying to figure out how to draw the domain on a number line. I am trying to figure out how to use a number line to find the domain.

 

[MarkFL]

Whoops! Thank you, I had gotten the answer from my professor beforehand. There should be a way to figure out the problem without using an inequality though. That is what I am trying to understand how to use. I know it involves a number-line and, it seems like, you guess at possible values for x. For example, you couldn't find the domain of $$y = ln\frac{x - 1}{(x - 3)(x + 5)}$$ just by using inequalities right? I am trying to figure out how to find the domain of a logarithm like that. The approach should work regardless of whether you use this or the first logarithm I posted. I am not just trying to figure out how to draw the domain on a number line. I am trying to figure out how to use a number line to find the domain.

For that function, we would set:

$$\frac{x-1}{(x-3)(x+5)}>0$$

To solve this, we need to find all of the roots of the numerator and denominator and list these as our critical values:

$$x\in\{-5,1,3\}$$

Because all of these roots are of odd multiplicity (the factors from which we obtained these roots are raised to an odd exponent, in this case all are to the first power), we know the sign of the expression will alternate across these critical values, and so we need only test one value of \(x\) in one of the resulting subdomains. For simplicity, I would choose \(x=0\) from the subdomain \((-5,1)\), and we find the expression is positive for that value of \(x\), and so that subdomain is part of the solution. And so the solution to the inequality, in interval notation, is:

$$(-5,1)\,\cup\,(3,\infty)$$

If you are more comfortable with testing a value in each subdomain, then you can do that...it's just less work if we realize the sign will alternate and simply test one.

And so the above is the domain of the function:

$$y(x)=\ln\left(\frac{x-1}{(x-3)(x+5)}\right)$$

 

[RidiculousName]

For that function, we would set:

$$\frac{x-1}{(x-3)(x+5)}>0$$

To solve this, we need to find all of the roots of the numerator and denominator and list these as our critical values:

$$x\in\{-5,1,3\}$$

Because all of these roots are of odd multiplicity (the factors from which we obtained these roots are raised to an odd exponent, in this case all are to the first power), we know the sign of the expression will alternate across these critical values, and so we need only test one value of \(x\) in one of the resulting subdomains. For simplicity, I would choose \(x=0\) from the subdomain \((-5,1)\), and we find the expression is positive for that value of \(x\), and so that subdomain is part of the solution. And so the solution to the inequality, in interval notation, is:

$$(-5,1)\,\cup\,(3,\infty)$$

If you are more comfortable with testing a value in each subdomain, then you can do that...it's just less work if we realize the sign will alternate and simply test one.

And so the above is the domain of the function:

$$y(x)=\ln\left(\frac{x-1}{(x-3)(x+5)}\right)$$

It looks like I'll need to get help from my professor with this one. Thank you anyway. I'm just really having a hard time understanding what you're saying. Also, it seems like you're going over a method that relies on the factors of the roots being raised to odd exponents, which, I think, isn't what my professor was discussing. I really have no idea about most of what you're saying anyway. Like, how do you know [1, 3] isn't part of the domain? What is a critical value? What do you mean the sign will alternate?

 

[MarkFL]

It looks like I'll need to get help from my professor with this one. Thank you anyway. I'm just really having a hard time understanding what you're saying. Also, it seems like you're going over a method that relies on the factors of the roots being raised to odd exponents, which, I think, isn't what my professor was discussing. I really have no idea about most of what you're saying anyway. Like, how do you know [1, 3] isn't part of the domain? What is a critical value? What do you mean the sign will alternate?

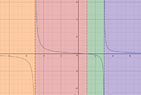
Let's take a look at a graph of the expression which is the argument for the natural log function:

$$y=\frac{x-1}{(x-3)(x+5)}$$

View attachment 8432

The critical values are values for which either the numerator or denominator are zero (roots) and as I stated, these are:

$$x\in\{-5,1,3\}$$

These 3 critical values will divide the real numbers into 4 intervals, which are shaded in the diagram above. These intervals are:

$$(-\infty,-5)$$ shaded in orange

$$(-5,1)$$ shaded in red

$$(1,3)$$ shaded in green

$$(3,\infty)$$ shaded in blue

Now, let's forget about the multiplicity of the roots, and choose a test value from each of the 4 intervals, and look only at the signs (positive + or negative -) of the factors in the expression

$$(-\infty,-5)$$ shaded in orange

In this interval, let's choose \(x=-6\) and so the signs of the 3 factors are:

$$\frac{(-)}{(-)(-)}=-$$

The expression is negative in this interval, and so it is not part of the solution, since we require the overall expression to be greater than zero, or positive.

$$(-5,1)$$ shaded in red

In this interval, let's choose \(x=0\) and so the signs of the 3 factors are:

$$\frac{(-)}{(-)(+)}=+$$

The expression is positive in this interval, and so it is part of the solution.

$$(1,3)$$ shaded in green

In this interval, let's choose \(x=2\) and so the signs of the 3 factors are:

$$\frac{(+)}{(-)(+)}=-$$

The expression is negative in this interval, and so it is not part of the solution.

$$(3,\infty)$$ shaded in blue

In this interval, let's choose \(x=4\) and so the signs of the 3 factors are:

$$\frac{(+)}{(+)(+)}=+$$

The expression is positive in this interval, and so it is part of the solution.

Do you see how the sign of the expression alternated over each interval?

And so the solution to the inequality:

$$\frac{x-1}{(x-3)(x+5)}>0$$

is the union of all the intervals we found to be part of the solution:

$$(-5,1)\,\cup\,(3,\infty)$$

And this then is the domain of the function:

$$y(x)=\ln\left(\frac{x-1}{(x-3)(x+5)}\right)$$