Finding the eigenfunction of momentum

[iScience]

the questions is: is the ground state of an infinite square well an eigenfunction of momentum, if so what is the momentum?

solution:

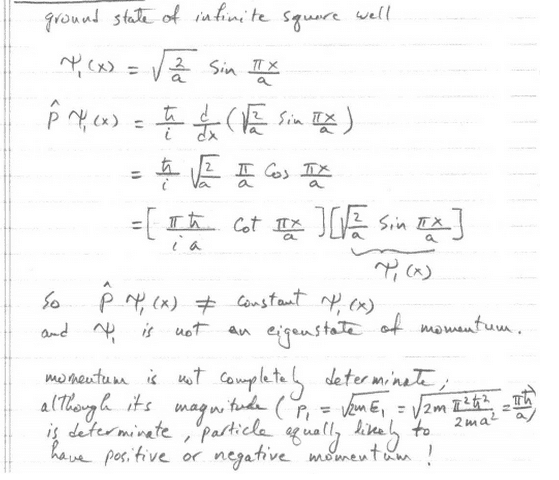
i was working it out and i got something different from the solutions, and i don't understand where they're getting the cotangent term from..


and also, please confirm this for me; the eigenvector is the wavefunction, the eigenvalue is the observable (in this case, the momentum), and the eigenFUNCTION is the operator right?

 

[tman12321]

The eigenfunction is the wavefunction (can also be called an eigenvector) and is the sine function here, the eigenvalue would be the observable (a number), and the operator in this case is momentum. If you have an operator P and a function f, f is an eigenfunction of P if P f = p f, where p is some number. If you take the derivative of sine, you don't get a number multiplying sine back; you get the cotangent term, which is not a constant. So sine is not an eigenfunction of P. An example of something that is an eigenfunction of P would be g = exp(i k x) for example. Then P g = hbar k g.

 

[wotanub]

What is $cot(x)sin(x)$?

The eigenvalue is the constant you get when you act the operator on a eigenvector/eigenstate/eigenfunction/eigenket/eigenmode/eigenface/etc.

The name you use depends on what is the most precise thing to say. For example, you'd say eigenfunction if you were talking about a wavefunction in the position representation, eigenstate/eigenket if you're still in abstract bra-ket notation, and you'd use the word eigenvector if say for example you were in a linear algebra class working out an eigenvalue equation. But also, the word "eigenvector" is technically always correct in any case since when you solve these types of equations, there is a map to some vector space in the abstract sense.

The operator is the momentum operator
The eigenvector is a momentum eigenstate (which you can write in a specific basis to call it an eigenfunction)
The eigenvalue is the momentum