Finding the final speed of a Positive and Negative Charge

[Abu]

Homework Statement

This is an example problem I found on khan academy and it didn't have an official problem statement... So I am going to have to make up my own problem statement from what was given. I can link the video if any of you want to see it.

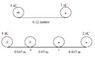
A positive charge 4uC and a negative charge 2uC, both with a mass of 1kg, are placed 12 cm apart from each other. Find their final speeds when they are 3 cm apart from each other

Homework Equations

w = v * q
f = K q1*q2/r^2
v = K q/r
F = ma
Vf^2 = Vi^2 + 2ad

The Attempt at a Solution

I know the real solution to this problem as it was shown in the video that I watched to get this example. But my question is how come my solution does not work.

What I attempted to do was:

F = K q1*q2/r^2
F = 9*10^9 (4*10^-6) (2*10^-6)/0.12^2
F = 5 N
This is the force of attraction between the two charges
F = ma
5 = 1a
a = 5m/s^2 since the mass of each charge was 1kg in the problem (I realize 1kg is an absurd mass)
Vf^2 = Vi^2 + 2ad
Vf^2 = 0 + 2(5)(0.045) I did 0.045 because if they are 0.03m apart then that means they each traveled 0.045 m
Vf = 0.67 m/s

Now this answer is incorrect. I can post the link to the video I got the problem from. It is the second/final problem in the video. Their solution uses conservation of energy. It starts at 10:30, and their final solution was 1.3 m/s



Here is why I think my solution is wrong: The acceleration is not constant, because as their charges move closer together, the force of attraction is stronger and thus their acceleration increases.

Is there any way I can correct my answer by still using the force of attraction method? Can I do the change in force from their initial positions to when they are 3 cm apart - or is the conservation of energy method the only way?

If you would like me to clarify anything please let me know. Thank you.

 

[RedDelicious]

You are correct in that your answer is wrong because the acceleration is not constant. It is also wrong for another reason, though. The Coulomb force is an electrostatic force. That is, it is the force that a charge experiences when in an electrostatic field. These charges are accelerating and so this is a problem of electrodynamics and you would need to use the Lorentz force.

$$\vec{F}=q[\vec{E}+\vec{v}\times \vec{B}]$$.

Even if you're unaware of how complicated the fields turn out to be, I think you can get the idea that this approach will lead to an absolute mess that you would need to solve numerically.

That said, I have no idea how awful the approximation actually is, but you can use the Coulomb force anyway and treat it as a two body problem on a straight line, as is done in the case of gravity. This is how it is treated in the video, but the argument starts directly from energy considerations as opposed to dealing with the accelerations.

 

[Abu]

You are correct in that your answer is wrong because the acceleration is not constant. It is also wrong for another reason, though. The Coulomb force is an electrostatic force. That is, it is the force that a charge experiences when in an electrostatic field. These charges are accelerating and so this is a problem of electrodynamics and you would need to use the Lorentz force.

$$\vec{F}=q[\vec{E}+\vec{v}\times \vec{B}]$$.

Even if you're unaware of how complicated the fields turn out to be, I think you can get the idea that this approach will lead to an absolute mess that you would need to solve numerically.

That said, I have no idea how awful the approximation actually is, but you can use the Coulomb force anyway and treat it as a two body problem on a straight line, as is done in the case of gravity. This is how it is treated in the video, but the argument starts directly from energy considerations as opposed to dealing with the accelerations.

Sorry for the late response but I made another attempt after seeing your reply. I also drew a diagram because I thought it could help out:

Here is my second attempt at the problem:
The work/change in electric potential energy is denoted by w = Δv *q
This is w = (k q/r final - k q/r initial) * q2
So w = (9*10^9(4*10^-6)/0.03 - 9*10^9 4*10^-6/0.12) * 2*10^-6
w = 1.8 Joules
I know I am on the right track here because this is the same result as the video. However my next steps don't give me the right answer, they give me an answer close to it though:
w = f*d
1.8 = f*0.045
f = 40 N
a = f/m
a = 40/1 = 40m/s^2
Vf^2 = Vi^2 + 2ad
Vf^2 = 0 + 2(40)(0.045)
Vf = 1.897 m/s

This answer is close to the correct one 1.3 m/s. I know that we concluded my last answer was wrong because acceleration does not remain constant, but I thought maybe I could still use f = ma because the force, f, was found using the change in electric potential energy. Am I on the right track with my current thinking?

Thanks.

 

[RedDelicious]

No. You are still assuming a constant acceleration.

For this one dimensional problem

$$W = \int F(x)dx \neq F\Delta x$$

The force is non-constant and so you can't just pull it out of the integral.

If you want to use forces, you need to treat it as a 2 body problem and consider the fact the force depends on their changing separation. If you do that correctly, you get the same answer as the video.$$m\ddot r_1 = \frac{kq_1q_2}{(r_2-r_1)^2} \\~\\ m\ddot r_2 = \frac{-kq_1q_2}{(r_2-r_1)^2} \\~\\ m\ddot r_2-m\ddot r_1 = m\frac{d^2(r_2-r_1)}{dt^2}=m\ddot r \: ~\: \text{ where } r = r_2 - r_1 \\~\\ m\ddot r_2-m\ddot r_1 = \frac{-kq_1q_2}{(r_2-r_1)^2}-\frac{kq_1q_2}{(r_2-r_1)^2} = \frac{-2kq_1q_2}{r^2} \\~\\ m\ddot r = \frac{-2kq_1q_2}{r^2} \\~\\ \ddot r r^2 = - \frac{2kq_1q_2}{m}$$

From here, multiply both sides by $\dot r /r^2$ and use the identity $\dot r \ddot r = \frac{1}{2} \frac{d}{dt}(\dot r^2)$ and the fact that $dr = \dot r dt$ to simplify the integrals. From that you can get it in terms of their approach velocity which tells you what their velocities should be. Note that q1 and q2 are in terms of magnitudes as I've set it up.

 

[Abu]

No. You are still assuming a constant acceleration.

For this one dimensional problem

$$W = \int F(x)dx \neq F\Delta x$$

The force is non-constant and so you can't just pull it out of the integral.

If you want to use forces, you need to treat it as a 2 body problem and consider the fact the force depends on their changing separation. If you do that correctly, you get the same answer as the video.$$m\ddot r_1 = \frac{kq_1q_2}{(r_2-r_1)^2} \\~\\ m\ddot r_2 = \frac{-kq_1q_2}{(r_2-r_1)^2} \\~\\ m\ddot r_2-m\ddot r_1 = m\frac{d^2(r_2-r_1)}{dt^2}=m\ddot r \: ~\: \text{ where } r = r_2 - r_1 \\~\\ m\ddot r_2-m\ddot r_1 = \frac{-kq_1q_2}{(r_2-r_1)^2}-\frac{kq_1q_2}{(r_2-r_1)^2} = \frac{-2kq_1q_2}{r^2} \\~\\ m\ddot r = \frac{-2kq_1q_2}{r^2} \\~\\ \ddot r r^2 = - \frac{2kq_1q_2}{m}$$

From here, multiply both sides by $\dot r /r^2$ and use the identity $\dot r \ddot r = \frac{1}{2} \frac{d}{dt}(\dot r^2)$ and the fact that $dr = \dot r dt$ to simplify the integrals. From that you can get it in terms of their approach velocity which tells you what their velocities should be. Note that q1 and q2 are in terms of magnitudes as I've set it up.

I really appreciate your effort in helping me figure this out but unfortunately I don't understand integrals and calculus as I haven't had those courses yet. I assume the best I can do is simply learn to accept the conservation of energy method, correct?

Thank you very much.

 

[RedDelicious]

I really appreciate your effort in helping me figure this out but unfortunately I don't understand integrals and calculus as I haven't had those courses yet. I assume the best I can do is simply learn to accept the conservation of energy method, correct?

Thank you very much.

Yes, you'll just have to accept the energy method for the time being. There is no simple way to do it using the accelerations because the force is constantly changing. The approach you tried using the work to find the force and then the acceleration doesn't work either because that formula is only true when the force is constant.