titansarus
- 62
- 0
- Homework Statement
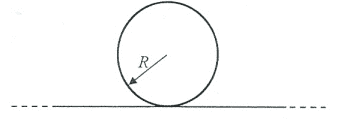
- We have a very big solenoid like the figure below. (it stretches outside and inside of the screen) It has radius ##R## and number of turns per length ##n##. A very large wire of length ##L>>R## is tangent to the solenoid and perpendicular to its axis (without physically connecting to the solenoid). The Current in solenoid is changing with rate ##\alpha = di/dt##. Find the induced emf on the wire. Note that it is a question of Undergrad General Physics and is not meant to be solved with very advanced mathematical techniques.
- Relevant Equations
- ##d \phi / dt = - \epsilon## ,##\phi = \int B da##
I know that ##B = \mu n I## and ##\phi = B \pi R^2##. So with have ##d\phi / dt = \mu n \alpha \pi R^2##. But I don't know what to do with this? is this the answer? I don't think so but I don't know what to do after this.