Finding the launch angle for a projectile if the range is 3x the max height of the trajectory

[member 731016]

Homework Statement

Please see below

Relevant Equations

Please see below

For this problem,

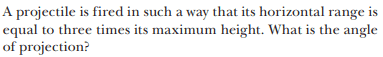
The solution is,

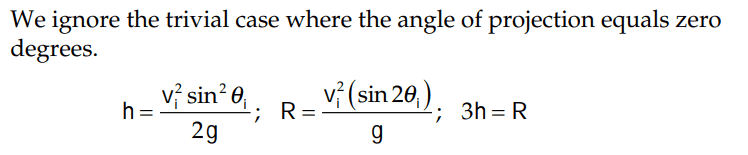
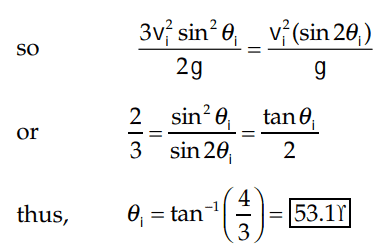
I don't understand how they got from $\frac {sin^2\theta_i}{sin2\theta}$ to $\frac{tan\theta_i}{2}$. Would somebody please show me the immediate steps?

I also don't understand is why they say the ignore the trivial case where $\theta_i = 0~rad$. Isn't it implied that $\theta > 0$ if $R = 3h_{max}$?

Many thanks!
Many thanks!

 

[TSny]

I don't understand how they got from $\frac {sin^2\theta_i}{sin2\theta}$ to $\frac{tan\theta_i}{2}$. Would somebody please show me the immediate steps?

Can you think of a trig identity for $\sin2\theta$?

I also don't understand is why they say the ignore the trivial case where $\theta_i = 0~rad$. Isn't it implied that $\theta > 0$ if $R = 3h_{max}$?

If $\theta_i = 0$, what would be the values of $R$ and $h$? Would $R = 3h$ be true? So, is $\theta_i = 0$ a solution?

 

[member 731016]

Can you think of a trig identity for $\sin2\theta$?If $\theta_i = 0$, what would be the values of $R$ and $h$? Would $R = 3h$ be true? So, is $\theta_i = 0$ a solution?

Thank you for your reply @TSny!

$sin 2\theta = 2\sin\theta\cos\theta$ Thanks, I see how they got $\frac{tan\theta_i}{2}$ now.

If $\theta_i = 0$, then $R = ∞~m$ (ignoring air resistance and friction) and $h = 0 m$, correct?

Many thanks!

 

[TSny]

If $\theta_i = 0$, then $R = ∞~m$

How do you deduce $R = \infty$ when $\theta_i$ = 0?

 

[member 731016]

How do you deduce $R = \infty$ when $\theta_i$ = 0?

Thank you for your reply @TSny!

Because if the angle with the horizontal is zero degrees, then won't you just be firing along the frictionless horizontal plane?

Many thanks!

 

[TSny]

Thank you for your reply @TSny!

Because if the angle with the horizontal is zero degrees, then won't you just be firing along the frictionless horizontal plane?

Many thanks!

Consider the range formula $$ R = \frac{v_i^2(\sin 2\theta_i)}{g}$$ in the limit as $\theta_i \rightarrow 0$.

 

[kuruman]

If $\theta_i = 0$, what would be the values of $R$ and $h$? Would $R = 3h$ be true? So, is $\theta_i = 0$ a solution?

A more informative statement than telling us to ignore the trivial solution would have been the stipulation that the projectile lands at the same height from which it was launched. It is necessary to establish the validity of the expression for $R$ that they use.

Aside from that, this question can be answered without fear of trivial solutions using equation (5) derived in this reference. The equation relates the three relevant angles in projectile motion,$$\tan\!\varphi=\frac{1}{2}(\tan\!\theta+\tan\!\omega).$$where all angles are relative to the horizontal and defined as
$\theta =$ angle of initial velocity vector (angle of projection)
$\varphi =$ angle of instantaneous position vector
$\omega =$ angle of instantaneous velocity vector
At maximum height, $~\tan\!\varphi=\dfrac{h_{max}}{R/2}~$ and $~\tan\!\omega=0.$ Substituting,$$\frac{h_{max}}{R/2}=\frac{1}{2}\tan\!\theta \implies \tan\!\theta=4\left(\frac{h_{max}}{R}\right).$$

 

[haruspex]

Thank you for your reply @TSny!

Because if the angle with the horizontal is zero degrees, then won't you just be firing along the frictionless horizontal plane?

Many thanks!

Yes, but that means it lands instantly.

 

[haruspex]

this question can be answered without fear of trivial solutions

Not possible. In the case of zero height, zero range, the angle is indeterminate. Therefore it must be explicitly excluded in the $\arctan(4/3)$ answer.
It follows that the equation you quote has been derived on the assumption of a nontrivial case.

 

[member 731016]

Thank you @TSny , @kuruman and @haruspex for your replies!

I understand now why the range is zero :) For some reason, I forgot the definition of range. I was thinking that while the projectile was sliding along the ground with no external forces acting, its range would increase to infinity.

 

[kuruman]

Not possible. In the case of zero height, zero range, the angle is indeterminate. Therefore it must be explicitly excluded in the $\arctan(4/3)$ answer.
It follows that the equation you quote has been derived on the assumption of a nontrivial case.

Indeed, the equation I quoted was derived on the assumption that a projectile has been fired and transited from point A to point B. It was not derived for projectiles that are at rest on the Earth. The derivation introduces the tangent as the ratio of the velocity components and is zero when the projectile stays on the ground ($v_{0y}=0$).

In any case, this problem clearly states that "A projectile has been fired in such a way . . . etc. " Why be concerned about trivial solutions, in situations where the statement of the problem implicitly excludes them? I think that the statement in the posted answer "we ignore the trivial case where the angle of projection equals zero degrees" is included because they want to justify the cancellation $$ \frac{3v_i^2\sin^{\cancel 2}\!\theta_i}{2g}=\frac{v_i^2(2\cancel{\sin\!\theta_i}\!\cos\!\theta_i)}{2g}.$$ However, I am puzzled by the inconsistency in rigor. When they cancel terms, on one hand they bring up the trivial case $\theta_i=0$ and then exclude it and on the other hand they completely ignore the trivial case $v_i=0$. Are some trivial cases more trivial than others?

 

[haruspex]

Indeed, the equation I quoted was derived on the assumption that a projectile has been fired and transited from point A to point B. It was not derived for projectiles that are at rest on the Earth. The derivation introduces the tangent as the ratio of the velocity components and is zero when the projectile stays on the ground ($v_{0y}=0$).

In any case, this problem clearly states that "A projectile has been fired in such a way . . . etc. " Why be concerned about trivial solutions, in situations where the statement of the problem implicitly excludes them? I think that the statement in the posted answer "we ignore the trivial case where the angle of projection equals zero degrees" is included because they want to justify the cancellation $$ \frac{3v_i^2\sin^{\cancel 2}\!\theta_i}{2g}=\frac{v_i^2(2\cancel{\sin\!\theta_i}\!\cos\!\theta_i)}{2g}.$$ However, I am puzzled by the inconsistency in rigor. When they cancel terms, on one hand they bring up the trivial case $\theta_i=0$ and then exclude it and on the other hand they completely ignore the trivial case $v_i=0$. Are some trivial cases more trivial than others?

I agree, but, arguably, "A projectile has been fired" excludes $v_i=0$ but not $\theta_i=0$.

 

[member 731016]

Thanks for your replies @kuruman and @haruspex !