Finding the magnitude of the electric field from 3 charges at a point P

[KKuff]

Homework Statement

Hi, here is the problem I'm having trouble with:
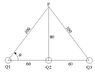
Three charges Q1, Q2, and Q3, each equal to 6.4 × 10–19 C, are in a straight line. The distance between neighboring charges is 60 nm. Find the magnitude of the electric field at P, which is 80 nm from Q2 on a line at right angles to the line between Q1 and Q3

Homework Equations

E = kQ/r²

The Attempt at a Solution

The correct answer is 1.9 x 10⁶ N/C, but I cannot figure out how to arrive at that answer.
I started by first finding the magnitude of the electric field from each charge
E1 = kQ1/r² = (8.99 x 10⁹ Nm²/C²)(6.4 x 10^-19C) / (100 x 10^-9m)² = 575360 N/C

E2 = kQ2/r² = (8.99 x 10⁹ Nm²/C²)(6.4 x 10^-19C) / (80 x 10^-9m)² = 899000 N/C

E3 = kQ3/r² = (8.99 x 10⁹ Nm²/C²)(6.4 x 10^-19C) / (100 x 10^-9m)² = 575360 N/C

Then I tried splitting those into the x and y components
E_x = 0, since E1_x and E3_x cancel each other out and there is no x component of E2

E1_y = 575360sin$\theta$ = 345216 N/C
E3_y would also equal this
E2_y = 899000 N/C

E_y = 1589432

so to find the magnitude of the resultant vector...
E = $\sqrt{}$(E_x² + E_y²)
E = $\sqrt{}$(0² + 1589432²) = 1589432
E = 1.59 x 10⁶

So what am I doing wrong here? Any help would be appreciated

 

[gneill]

The magnitudes of the fields for the three charges look okay, but the values you've calculated for the y-components of charges Q1 and Q3 don't look right. Check the angle you've used in the sine function.

 

[KKuff]

Hi, thanks for the reply, I got sin$\theta$ = 0.6, using the dimensions of the right triangle with the distance between Q1 and Q2 being 60nm and the distance between Q2 and P being 80nm, so the hypotenuse would be 100nm 60² + 80² = 100². Then sin$\theta$ = 60nm / 100nm. Is this wrong?
Thanks

 

[gneill]

sin(θ) = 80/100

 

[KKuff]

Thanks, I was using the wrong angle. In the future, how should I go about choosing the correct angle?

 

[gneill]

Thanks, I was using the wrong angle. In the future, how should I go about choosing the correct angle?

You can use either angle as long as you use the correct trig function! The trig functions are just ratios, as you know.

When you've got all the side lengths for the triangle (as you do in the case of this problem) it's probably easier to just form the correct ratio directly from it; Choose the side that lies in the same direction as the vector component you're looking for and divide by the hypotenuse.