Well, take your picture. There are 5 particles and the sum of energies is 13 x E1, so it doesn't qualify for the answer, but as an example: let's count the number of ways we can arrange these particles over the four energy levels.
- - -
Now I think we need to have some more information to do this right. If this is a course in statistics with numbered lottery balls (it is not, I think), the situation is different from e.g. a course in quantum mechanics with bosons that are
indistinguishable. My story continues below with that last assumption. The context makes it higly probable, the answer justifies it.
Furthermore, your formulation of the problem causes some confusion: you want to count the number of accessible microstates, and a little further it says: several particles can occupy the same microstate.
I propose to use the word state (or eigenstate) in the latter case: a solution with a certain energy associated. Several solutions can have the same energy.
And the word microstate is for a unique distribution of the particles over the states.
There is an expression for what ?
Well, for counting the number of possible microstates, given a certain distribution of the particles over the energy levels! Something to do with factorials, permutations, and so on. Either they are in the section preceding the exercise in your book, or you can check out e.g. http://www.pma.caltech.edu/~mcc/Ph127/a/Lecture_13.pdf
A few casual observations: if we have five big bottles for five lotto balls (that would be all particles in level 4, so an energy of 20 x E1, NOT in our cherished 450) we get how many microstates? Yes, 5^5 (five possibilities for ball 1, idem 2,3,4,5). Big number. You know this.
Same exercise with indistinguishable steel balls: Naive approach: Big number divided by the number of permutations of the five balls (5!=120) , perhaps ? No way: quotiënt is not an integer! Took me some time to figure out what the link mentions under
bosons. (That's why this response took a while...)
- - -
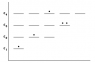
Back to your picture:
E5: 5 ways
E2: 3 ways
E3 is the hard one: particle 1 4 ways, particle 2 4 ways also, so 16 times, but now we did some double counting, for which we have to correct: if both are in the same state it's ok, the others were double counted, so 4 + (16 - 4)/2 = 10. Phew...this gets awkward, so
understanding the 'trick' in the link is a life saver here...
E1 is a giveaway: only one way to do this.
5 x 3 x 10 x 1 would be my guess for the number of possible microstates in your drawing. Pretty large number.
Your exercise:
Still a lot of work. How many ways have you found to get n1 + n2 * 2 + n3 * 3 + n4 * 4 = 12 ? Persevere and the 450 is yours! Important concept, nice exercise.